Basics

• A <- c(1:10) creates the list (1,2,3,...,10) and assigns it to variable A.
• sum(A), mean(A), min(A), and max(A) do what you expect.
• A^2 and A-mean(A) produce lists; what does mean((A-mean(A))^2) produce?
• What do var(A) and sd(A) produce?

Distributions

R has many built-in distributions. Each distribution can be accessed using functions with one of 4 prefixes: d, p, q, or r. They refer to density/mass, cumulative probability, quantile, and sampling. Try the following:

• pdf <- dbinom(c(1:16), 16, 0.7)
• barplot(pdf, main="Binomial probabilities; n=16 p=0.7", xlab="Number of successes", names.arg=c(1:16))
• for (p in c(.005, .025, .05)){print(qnorm(1-p))}
• rand <- rnorm(100, 50, 4)
• hist(rand)
• qqnorm(rand)
• Generate 99%, 95%, and 90% confidence intervals for the mean based on rand

The power function problem

In class we looked at using a random sample of size 16 from a Bernoulli population to test the null hypothesis H₀: θ = 0.75 against the alternative H₁: θ ≠ 0.75. We decided to reject the H₀ in favor of H₁ if X, the total number of successes in our sample, was any number other than 11, 12, or 13. Your first job is to get R to give you a graph of the power function of this test. Then do the same, but with a different critical region: reject H₀ if X isn't 12, 13, or 14. Compare the power functions of the tests. Some sample code to help you get going:

• x <- seq(0, 1, length=101)
• y <- pbinom(10, 16, x)
• plot(x, y, type='l')

Data input

• scan() can be a nice way to enter lists (manually or copy and paste).
• read.csv('filename.csv') and read.table('filename.txt', sep='\t', header=TRUE) are useful for getting existing data into R.
• You may need to change the working directory using setwd("path/to/desired/directory") (you can check on the working directory using getwd()).
• Download 422-S18 Height data and give it a better name (like height.csv).
• Load the data into R and name it h: h <- read.csv('height.csv').
• Give the columns better names: colnames(h) <- c("Back", "Front").
• summary(h) summarizes the data.
• plot(stack(h)[, 2:1]) gives us a boxplot.
• t.test(h$Back, h$Front) runs a hypothesis test.
• Kaggle seems like an interesting source of data (login required).

Linear regression

• Load scores.csv into R (if not already loaded): scores<-read.csv('scores.csv')
• plot(scores$A1,scores$A4, col="blue", main="Scores on Exam 1 and Exam 4 in Math 157", xlab="Exam 1 Score", ylab="Exam 4 score")
• m<-lm(scores$A4~scores$A1)
• abline(m)
• summary(m)
• plot(m)
• Repeat for section B
• Repeat for the combined scores of both sections

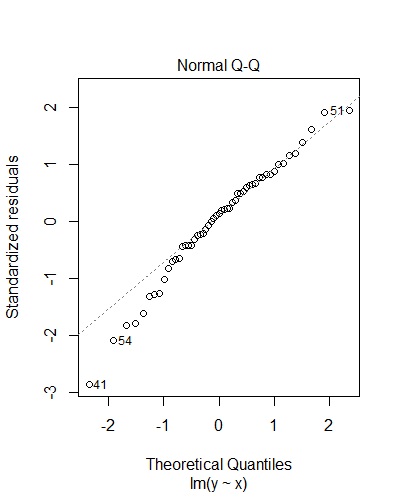
• > summary(m)
  
  Call:
  lm(formula = y ~ x)
  
  Residuals:
      Min      1Q  Median      3Q     Max 
  -33.674  -5.261   1.626   7.764  22.590 
  
  Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
  (Intercept)  21.3822     8.9714   2.383   0.0209 *  
  x             0.7125     0.1119   6.369  5.4e-08 ***
  ---
  Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
  
  Residual standard error: 11.89 on 51 degrees of freedom
    (7 observations deleted due to missingness)
  Multiple R-squared:  0.443,	Adjusted R-squared:  0.4321 
  F-statistic: 40.56 on 1 and 51 DF,  p-value: 5.396e-08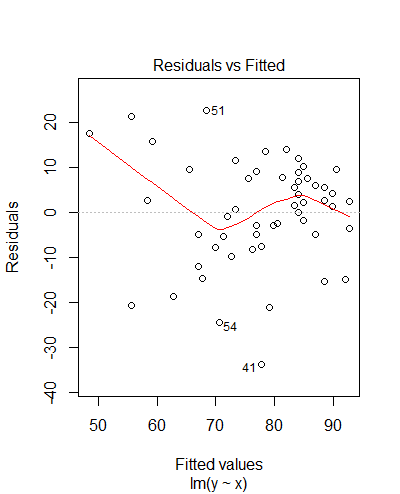

  
• Multiple linear regression is also possible. Here LE is Life Expectancy, CU is the rate of Contraceptive Use, and H is Health care expenditures (all from the CIA World Factbook). Be careful of confounding.

      > summary(model)
      
      Call:
      lm(formula = data$LE ~ data$CU + data$H)
      
      Residuals:
      Min       1Q   Median       3Q      Max 
      -22.3880  -2.8498   0.3035   3.3646  16.8333 
      
      Coefficients:
      Estimate Std. Error t value Pr(>|t|)
      (Intercept) 56.10052    1.63577  34.296   <2e-16 ***
      data$CU      0.24304    0.02562   9.485   <2e-16 ***
      data$H       0.24974    0.19161   1.303    0.195
  						     

• The Hmisc library gives a nice way of looking at the correlations between our variables.

      > rcorr(as.matrix(data[2:4]))
  	
  	LE   CU    H
      LE 1.00 0.66 0.25
      CU 0.66 1.00 0.25
      H  0.25 0.25 1.00
  
      n= 134 
  
      P
         LE     CU     H     
      LE        0.0000 0.0035
      CU 0.0000        0.0030
      H  0.0035 0.0030       
  

Analysis of variance

• Download old height data and load it into R: h <- read.csv("height_data.csv")
• I found it helpful to rename the columns: colnames(h) <- c("section", "sex", "c", "m", "f")
• Interpret the results of model <- lm(h$c~h$m+h$f)
• Load the Hmisc library (library(Hmisc)) and determine if the output of rcorr(as.matrix(h[3:5])) affects your analysis of the previous linear regression model
• Fit a model (m <- lm(h$c~h$sex)) and compare summary(m), anova(m), and t.test(h[h$sex == "M", 3], h[h$sex == "F", 3])
• Use a summary or an ANOVA to interpret lm(h$m~h$sex)
• Compare plot(h$c~h$sex) and plot(h$m~h$sex)
• lm(c~section+sex, data=h) should allow you to run a 2-way ANOVA
• Run a 2-way ANOVA on the lion hunting data in R HW 1
• Check the validity of your models (using plot(model) and/or hist(residuals(model)))
• For more, see this summary from Columbia University

Non-parametric tests

• I've heard that the average Gonzaga student lives less than 200 miles from Gonzaga. Assume the class constitutes a random sample and test the claim. Use a t test if the data seems to be approximately normal (hist and qqnorm might be useful). Otherwise use Wilcox.test (you might use help(wilcox.test) to see how the test works).
• The immer data set gives barley yields for 2 years (1931 and 1932) in a variety of fields and varieties. First load the data with library(MASS) and look at the structure with head(immer). I'd like to know if the two years had the same average yield. Which of the following tests should I use?
  • t.test(immer$Y1, immer$Y2)
  • t.test(immer$Y1, immer$Y2, paired=T)
  • t.test(immer$Y1-immer$Y2)
  • wilcox.test(immer$Y1, immer$Y2)
  • wilcox.test(immer$Y1, immer$Y2, paired=T)
  • wilcox.test(immer$Y1-immer$Y2)
• The Wilcoxon test is appropriate for comparing two populations, as in this example
• The Kruskal-Wallis test compares multiple populations. Run kruskal.test(immer$Y1~immer$Var) and kruskal.test(immer$Y1~immer$Loc) and interpret the results. (I always like to see plots, so I also run plot(immer$Y1~immer$Var) and plot(immer$Y1~immer$Loc)).
• Compare cor.test(immer$Y1, immer$Y2) with cor.test(immer$Y1, immer$Y2, method="spearman").
• What else can you do with this data?

Resources/Links

• R Companion
• R cheat sheet (credit to ?)
• Verzani's simpleR
• Dr. Burch's R notes
• Free intro to R (login required)
• Virtual Laboratories in Probability and Statistics
• Up to Math 422

Office hours

• Monday 1:30-2:30
• Tuesday 10:00-11:00 in the Math Lab
• Wednesday 1:30-2:30
• Thursday 10:00-11:00
• or by appointment

Logan Axon
Department of Mathematics
MSC 2615
Gonzaga University
Spokane, WA 99258
Office: Herak 307A
Phone: 509.313.3897
Email: axon@gonzaga.edu

Last updated 9/24/18