Calculus II, Ice Cream Cone Challenge
Congratulations, you are about to open a new ice cream parlor! In preparation for this business adventure, you
are hoping to design a spill-free cone. You've constructed the cone, and decided on a base angle of 30 degrees, since
it is the most comfortable angle to hold. The height of the cone is 1 unit. What remains to decide is how best to
scoop the ice cream in order to keep it from spilling over the edges of the cone.
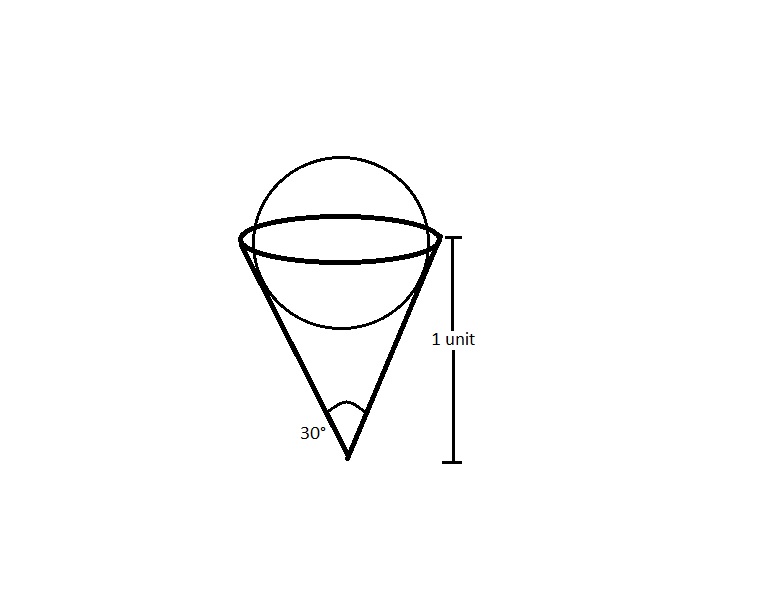
1) What radius of (spherical) scoop of ice cream will give you the most volume of ice cream inside the cone
(as opposed to above the cone)?
2) What percent of this sphere of most volume lies inside the cone?
You should be careful in choosing variables that help you answer this question. When you have determined the optimal radius,
be sure to make an accurate drawing of your sphere in the cone to insure the reasonableness of your result.
Figured it out? Excellent! Now share your spill-proof cone with the world...
• You should write up your results in a short paper (2-3 pages is appropriate). Be sure to include all details
of your calculations (including clear definition of all variables and functions used) and to explain your process.
Your solution should be written clearly in english with correct grammar.
• Include diagrams as appropriate to illustrate your variables as well as to demonstrate the reasonableness of
your solution. Be as accurate as possible.
• Include all relevant calculations in as much detail as you can, including explanation.
• You are encouraged to type your paper if possible. The program LaTeX is the best way to type mathematics. You can
learn how to use it from this wikibook, and the resources listed below.
You are not required to use LaTeX for this project, but it will likely be the best way to incorporate your calculations in your
paper. You can also explore the option of Microsoft Word's equation editor. If you are uncomfortable using either of these,
you may hand-write your paper. You will be required to submit the paper electronically. If you decide to hand-write the
paper, please scan your paper to submit it.
• Bonus As good as ice cream is, this problem (or very similar ones) can be applied to more practical situations.
In the conclusion of your paper, describe a practical application of a calculation similar to this one.
You may work with a partner or small group on this project, you may also work on it alone. If you choose to work with
others, a grade will be assigned to the group collectively. Your grade on the project will be based on the mathematical
content of your paper (50%) as well as your ability to effectively communicate mathematics (50%). The final write up is due
Friday, May 1 by 5 pm, and should be submitted electronically by e-mail to your professor.
LaTeX resources
Here are some other resources about working with LaTeX:
• Cloud-based LaTeX computing is available at www.writelatex.com
and www.sharelatex.com.
• DeTeXify can help you find a symbol you need
to use.
• TeX Stack Exchange is a Q&A site with descriptions of
some of the more complicated TeXing techniques.
• The Comprehensive
LaTeX symbols list.
• Symbol Search
• A general
introduction
• Another brief introduction
