GENERAL CHEMISTRY TOPICS
Electromagnetic radiation and waves
Electromagnetic (EM) radiation. The EM spectrum. The wave nature of EM radiation; description and characteristics of waves.
Electromagnetic (EM) radiation
- Visible light is a particular form of electromagnetic (EM) radiation
- Other familiar forms of energy transmission, such as radio, microwaves, infrared radiation, ultraviolet (UV) light, and X-rays are all different forms of EM radiation
- All EM radiation can be described as waves.
- Each type of EM radiation is defined by a particular range of wavelengths
- All EM radiation travels at the speed of light, c (c = 2.99792458 × 108 m·s−1)
- The fundamental relationship for EM waves is frequency × wavelength = speed, or νλ = c
The latter relationship follows from a similar equation above
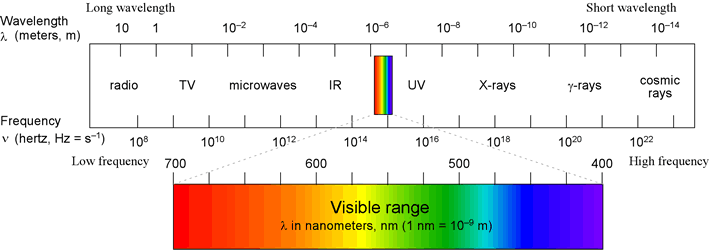
that holds for all traveling waves. Below is an illustration of the entire
EM spectrum. Note the inverse relationship between frequency and wavelength.
Low frequency, long wavelength forms of EM radiation are shown on the left,
and as one moves toward the right, frequency increases and wavelength decreases.
The forms of EM radiation with the highest frequency and shortest wavelengths
are shown on the right side of the figure.
Visible light occupies a relatively narrow portion of the spectrum, in the middle,
with wavelengths between 700 nm (red) and 400 nm (violet)
Waves
If EM radiation can be described as waves, what are the characteristics of waves? Waves show a repetitive or periodic form. Waves do not have mass, but they do carry energy, and they are able to propagate - that is, travel - though some medium. All propagating (traveling) waves have four basic characteristics: speed, frequency, wavelength, and amplitude. We can represent waves mathematically, in a graph form, as shown below.
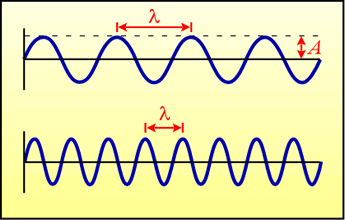Left: Two waveforms, with the wavelength (λ) and amplitude (A) indicated.
Note that the wave is a repeating series of peaks and valleys. To visualize the idea of the speed of the wave, imagine that the figure is showing a snapshot of the wave at one instant of time, and that the whole repeating waveform is moving from left to right. From the perspective of a fixed point on the x axis (the horizontal line), we would see a succession of peaks and valleys passing by. The frequency of the wave would be given by the number of peaks (or valleys) that we see passing us per unit of time.
The wavelength is defined as the distance between equivalent points on the repeating waveform - such as the distance between two successive peaks. Wavelength is conventionally represented by the Greek letter lambda (λ). The figure shows waveforms of two different wavelengths - the lower wave has a shorter wavelength than the top wave. If both waves are traveling at the same speed, then in observing the bottom wave from a fixed point, we would see more peaks passing us per unit time than if we were watching the top wave. Thus, the bottom wave would have a higher frequency than the top wave. The frequency of a traveling waveform, usually denoted by the Greek letter nu (ν), apparently has an inverse relationship with wavelength: as the frequency increases, the wavelength decreases, and vice-versa. In fact, an important relationship that holds for all waves is the following:
speed of wave = (frequency) × (wavelength) or speed = ν λ
One of our principal objectives is to use this relationship to convert between frequency and wavelength for any given value of either of these. We may also find it necessary to use decimal multipliers for unit conversion, as frequencies and wavelengths of EM radiation vary over many orders of magnitude.
Example: What is the frequency (ν) of visible light with wavelength λ = 535 nm?
Solution: We'll use c = 2.99792458 × 108 m·s−1 and a rearranged form of the relation between c, ν, and λ:
ν = c / λ
Since wavelength is given to us in nm, the conversion from nm to m must be included in our calculation:
ν = (2.99792458 × 108 m·s−1) / (535 nm)(10−9 m/nm) = 5.60 × 1014 s−1
In this context, the unit s−1 gets a special designation, hertz (Hz), so we will write the answer as 5.60 × 1014 Hz.
As stated above, waves carry energy, but how much energy? The energy a wave carries is related to its amplitude, which is one-half the distance between the wave's crest (highest point) and trough (lowest point). We can readily agree that a tsunami carries much more energy than a pond ripple. The amount of energy delivered by traveling waves such as ocean waves, sound waves, or the waves of EM radiation is time-dependent, so we can alternatively relate wave amplitude to power, or energy per unit time. The power carried by a wave is proportional to the square of its amplitude and the square of its frequency. A related quantity, intensity (I) is defined as the power transmitted by the wave per unit area normal to the direction of propagation. (Waves such as light or sound from a point source are three-dimensional, as opposed to the one-dimensional waveform shown above.) The intensity of a wave is also proportional to the square of the wave amplitude.
Mathematics of waves
We can write the equation
y = A sin (2πx/λ)
for the stationary waveforms shown above, with A the amplitude of the wave, and λ the wavelength. Over the interval for x from 0 to λ, this wave function makes a complete cycle. In the next interval, x = λ to x = 2λ, the function repeats, and so on for each succeeding interval of length λ. Such repeating functions are termed periodic functions. We can introduce a phase factor into the waveform by adding a term to the argument of the sine function. (The argument is the expression inside the parentheses that gives the value that one would "take the sin of". Another way of saying this is that the argument of a function [such as exp, log, sin, cos,...] is the expression or value the function operates on.) Including a phase factor Φ gives us
y = A sin { 2π [(x/λ) − Φ] }
For a traveling wave, the waveform changes position with time. Thus time must be included as a variable in the argument of the trigonometric function. If we denote the constant speed of the traveling wave as u, then the wave will travel a distance x in time t = x/u.
The equation obtained by this substitution of variables does not change the waveform graph plotted above, but simply scales and re-labels the horizontal axis. What if we want time and position to be independent variables? We could introduce time as a phase factor:
y = A sin {2π[ (x − t) / λ ] }
Interference and diffraction
One of the characteristics of waves is they show interference. If two waveforms with the same wavelength are added together, the result depends on their relative phase.
Light and other forms of EM radiation show diffraction, which is a result of interference, and this is evidence that EM radiation is made up of waves.
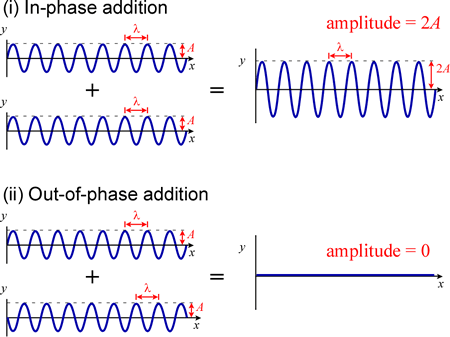
In-phase waveforms are shown adding together constructively, and out-of-phase waveforms canceling. In (i), two waveforms with the same wavelength λ and the same amplitude A add together to give a waveform with wavelength λ amplitude 2A since they are in phase - the crests and troughs of the two waveforms line up exactly along the x axis. In (ii), the bottom waveform is displaced along the x axis relative to the top waveform by exactly λ/2. The crests (maxima) of the top waveform then line up exactly with the troughs (minima) of the bottom waveform, and the waves cancel.
The form of electromagnetic waves includes both an electric and a magnetic component. The electric component is an oscillating electric field, or electric field wave, and the magnetic component is also an oscillating magnetic field. These oscillations (waves) travel in the same direction and at the same speed (c), have the same wavelength, are in phase, but are oriented perpendicular to one another.
Interaction of matter with light
Our everyday experience is infused with the constant interplay of matter and energy. Our very capacity for sight is fundamentally based on specialized molecules that absorb the energy of incident light, which begins a process by which we sense brightness, color, and all the spatial qualia of our environment. The colors we perceive are due to the specific wavelengths within the visible range that are transmitted through, reflected or scattered, or emitted by matter. The emission of light by matter can be incandescence, the glow given off by matter at a high temperature, or luminescence, in which matter at normal or low temperature gives rise to light. Luminescence can have a variety of origins, among them are chemical reactions and radioactivity, but mainly we are concerned with photoluminescence, in which EM radiation of certain wavelengths are absorbed by matter, which re-emits the radiation, typically at longer wavelengths. In order to explain the experimentally observed details of these phenomena, we must examine the quantum nature of both EM radiation and the atom, which govern the interaction of matter with light.