GENERAL CHEMISTRY TOPICS

Kinetic molecular theory

Theoretical treatment of an ideal gas using the macroscopic laws of mechanics and statistics

---

In kinetic molecular theory (sometimes referred to more simply as "kinetic theory"), an ideal gas is treated as a vast collection of tiny particles, which we can model as spheres, that exert pressure according to the sum of their collisions with the walls of their container. Given the postulates of kinetic theory, a statistical treatment of the particles (atoms or molecules) that make up a gas leads to the ideal gas law and the relationship of temperature to the average particle kinetic energy.

The kinetic molecular theory of gases

The basic postulates of kinetic molecular theory can be given as follows³:

1. A pure gas consists of a large number of identical particles (molecules), separated by distances that are large compared with their size.
2. The molecules of a gas are constantly moving in random directions with a distribution of speeds.
3. The molecules of a gas exert no forces on one another except during collisions, so that between collisions they move in straight lines with constant velocities.
4. The collisions of the molecules with each other and with the walls of the container are elastic; no energy is lost during a collision.

These simple postulates about the nanoscale nature and behavior of a gas can be used to derive the bulk (macroscopic) physical properties of a gas, including the ideal gas law. In this approach we also gain a deep insight into the meaning of temperature. In the physical chemist's view, temperature is related to the average kinetic energy of the atoms and molecules that make up a macroscopic sample whose temperature we are measuring.

The large number of molecules is a key point – making statistical treatment valid and average values predictive. A statistical model is implied by 2nd postulate – molecular speed is a continuous random variable, and we can theoretically predict the distribution, and then look to see if the prediction is validated by experiment.

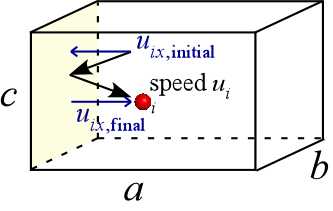
If we focus on one particle, (i), as shown at left, it travels with speed u_i. The speed in the x direction, which is the x component of the velocity vector u, is u_ix. This quantity changes in sign but not magnitude as a result of the collision with the left vertical wall. That is, if the initial speed of the ith particle along the x direction is −500 m s⁻¹, its final speed in the x direction will be +500 m s⁻¹. By the laws of physics, the force exerted on the wall by this collision will be the particle mass times the change in speed along the x direction divided by the time interval over which it occurs.

Writing this as an equation, we have

F_ix   =  mΔu_ix/Δt  =  m(2u_ix) / (2a/u_ix)  =  mu_ix²/ a        (1)

where we have set Δu_ix = 2u_ix and the time interval Δt is given by the time it takes for the particle to travel from the left vertical wall, to the right vertical wall, and back again. This is the frequency of collisions by particle i with the left vertical wall, and is equal to 2a/u_ix, the distance to be traveled divided by the speed in that direction. We can now write an expression for the force exerted on the left vertical wall by all N particles with the help of statistical reasoning.

We can replace the quantity u_ix with the mean-square speed along the x direction <u_x²>, which in turn is statistically equal to (1/3)<u²> (defined at right).

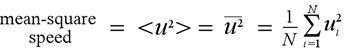
So for all N particles we can write

F_total   =  Nm<u²>/3a        (2)

Since pressure is force per unit area, we can easily substitute the area of the wall, bc, into the above expression, obtaining

P  =  Nm<u²>/3abc  = Nm<u²>/3V        (3)

since the volume of the container V = abc. Bringing volume to the left side of the equation gives us

PV  =  (1/3)Nm<u²>  =  (1/3)nM<u²>        (4)

where n is now the number of particles in moles, and M is the molar mass (kg mol⁻¹). We see that PV is constant as long as the mean-square speed of the gas molecules is constant. If we now compare this expression to the ideal gas law, we obtain a kinetic molecular theory interpretation of temperature. Substituting nRT for PV in eq.(4), we have

nRT  =  (1/3)Nm<u²>  =  (1/3)nM<u²>        (5).

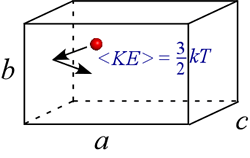
The average kinetic energy, <KE>, is given by ½·m<u²>, so we can write

nRT  =  (1/3)Nm<u²>  =  (2/3)N<KE>  =  (2/3)nN_A<KE>       (6).

By canceling out the common factor n, and solving either for T or average kinetic energy <KE>,

T  =  (2/3)(N_A/R)<KE>     or      <KE> =  (3/2)kT        (7)

where we have used the relation R = N_Ak. The constant k is thus the nanoscale version of the gas constant R, and is called the Boltzmann constant.

k  =  1.38066 × 10⁻²³ J·K⁻¹

Equation (7) shows that the temperature of a gas is directly proportional to the average kinetic energy of the molecules that make it up. The temperature so defined is the absolute temperature, and as the average kinetic energy of the molecules approaches zero, the temperature approaches absolute zero. This interpretation of temperature depends on the fact that the system of N gas molecules is not losing or gaining energy, even though the individual speeds may vary widely. This condition is one of thermal equilibrium, and is met when the surroundings (the walls of the container and the outside environment) are at the same temperature T as the system of N gas molecules.

The Maxwell-Boltzmann distribution of particle (atomic or molecular) speeds

A Maxwell-Boltzmann distribution describes the probability that a particle is moving with a particular speed at a given temperature, and we note how the distribution shifts to higher speeds as temperature increases.

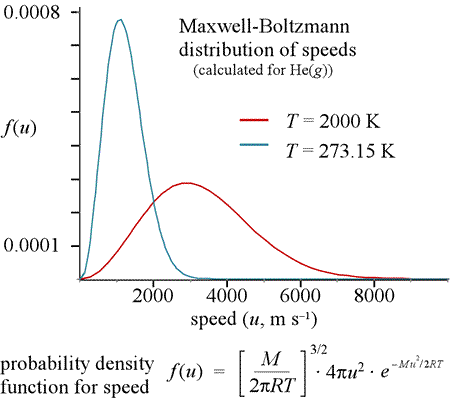
The Maxwell-Boltzmann equation (below the graph at left) is a probability density function for speed u. The equation includes the terms M, the atomic or molecular mass in kg/mol, R, the gas constant in J/K mol, and temperature T in K (kelvin). The graph shows the curves obtained for helium atoms at two different temperatures. Note the curves are not symmetric - there is more of an elongated "tail" at high speeds. The most probable speed (speed corresponding to the peak of the curve) will be a little less than the average speed, <u>. The entire area under the curve for a given temperature is the probability that a molecule is moving at some speed, which is a probability of 1. The probability that a molecule is moving at a speed within some range is the area under the curve between the speeds defining the range.

Note that the distribution function is independent of time, a feature that implies a condition of thermal equilibrium.

The Maxwell-Boltzmann distribution has relevance for many physical and chemical phenomena, such as phase changes (e.g. evaporation, sublimation) and chemical kinetics, specifically the theory of reaction rates. The distribution of speeds is closely related to a distribution of motional kinetic energy among molecules of a system. The kinetic energy of molecules can reside not only in their motion through space, but also in bond stretching, bending, and twisting. They also possess rotational kinetic energy. This didn't concern us in the modeling of an ideal gas, but is a crucial consideration in applying more broadly the ideas and results of kinetic molecular theory. Nonetheless, kinetic energy in these forms is constantly being redistributed by collisions between the molecules, and for our purposes, we can think of total kinetic energy of a system of molecules at a given temperature as having a distribution similar to that predicted by from the Maxwell-Boltzmann result.

It took nearly a century after Maxwell first derived the equation for the distribution of speeds (1860) for it to be confirmed by direct experimental measurement of molecular speeds (1955), an interesting example of theory in science far outstripping the ability of experimental methods to confirm or falsify its predictions.