Lecture 6. Periodicity and electron configurations

Thursday 1 February 2024

Electron configurations, valence electrons, and the Periodic Table for the elements. Orbital blocks. Electron configurations and elemental properties. Predictable ionic charges. Effective nuclear charge and periodic trends in atomic size.

Reading: Tro NJ.Chemistry: Structure and Properties (3rd ed.) - Ch.3, §3.5-3.6 (pp.134-142)

---

Summary

In the case of the hydrogen atom (and other one-electron species such as He⁺), the Schrödinger equation can be solved exactly. However, once we have to account for another electron or nucleus, the Schrödinger equation for such systems becomes unsolvable. We can, however, approximate solutions for many-electron atoms using the same orbitals and quantum numbers developed for the hydrogen atom. The principal difference is that orbital energies no longer depend on just n, but on both n and l.

Orbital energies for many-electron atoms

With a knowledge of the relative energies of electrons in atomic orbitals, we can use a few simple rules to generate the electron configurations of the elements. The diagram below represents the orbitals and their relative energy levels that will help us build up configurations for the first 36 elements. Also indicated are electron shells and orbital types and their relation to the quantum numbers. Orbital type (or shape) is specified by the angular quantum number, l. In fact, saying that an orbital is a p orbital is equivalent to saying the orbital has l = 1. Although we are oversimplifying the quantum mechanical model for atomic orbitals in describing the electron configurations of the atoms with the language of an electron shell model, the latter is nonetheless useful in capturing some of the important periodic trends in the chemical properties of the elements in a more readily visualizable way.

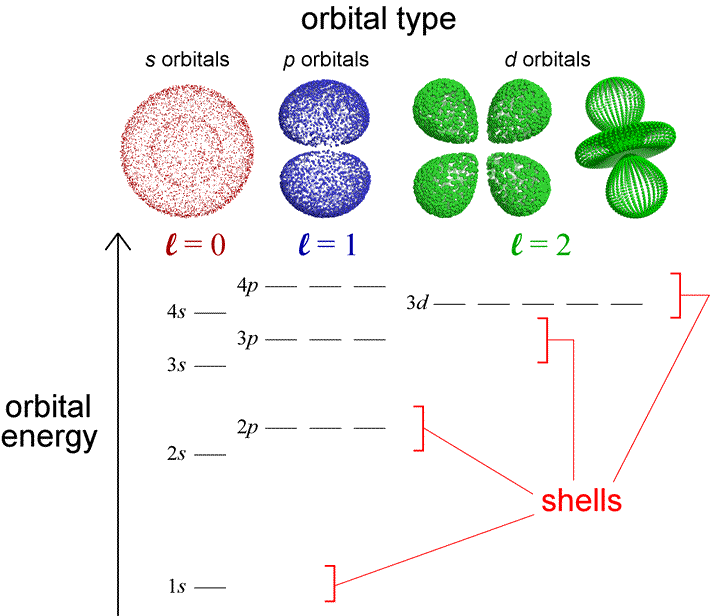
Let us use this diagram to review some important features of the quantum mechanical model of the atom and highlight the distinctions between the one-electron and the many-electron cases. The electron shell model of the atom divided electrons into core electrons and valence electrons, with the former closer to the nucleus and the latter the furthest out from the nucleus. In the quantum mechanical model for the atom, we know that the electrons are not literally confined to shells, but we can calculate a probability distribution for an electron in any orbital, and from that an average distance from the nucleus. For each set of orbitals with a fixed value for l, this average distance increases as n increases. Along with this there is an increase in the energy of the orbital, and this is reflected in the diagram. For example, the 4s orbital is higher in energy than the 3s orbital, which in turn is higher in energy than the 2s orbital, and so on. The many-electron case shares this feature with the one-electron case. But the diagram also shows that the energy of an orbital in a many-electron atom now depends on both n and l. Thus the orbital type or angular quantum number also help define a subshell, which are the orbitals of a given type or l value within a shell. The orbitals within a subshell all have the same energy (are degenerate). We see, for example, that 2p electrons constitute a subshell (l = 1) within the shell corresponding to n = 2. The dependence of orbital energy on both n and l affects the grouping of subshells within shells. The 3d electrons appear to be effectively part of a 4th shell, along with 4s and 4p electrons. How does this relate to the structure of the periodic table and correspond to the shell model? The valence electrons are all the electrons in the highest energy occupied shell. Core electrons are all electrons in the shell(s) below the highest energy occupied shell.

Orbital energy levels become more closely spaced as n increases. These energy levels are not fixed - they change with changing nuclear charge and depend on electronic occupancy. The relative energies shown will allow us to build up the correct electronic configurations for most of the first 36 elements and their common ions, but given the close spacing of 4s and 3d orbital energies, we will have to take care in predicting electron configurations for atoms and ions derived from 4th period elements, where there are some exceptions to our method of building up.

Nodes: An orbital will have n − 1 total nodes, with n − l − 1 radial nodes, and l angular nodes. The s orbital depicted is a 2s orbital, and the single node is a radial node. There are no angular nodes in any s-type orbital, since l = 0 for any s orbital. The p orbital depicted is a 2p orbital, which also has a single node, but in this case the node is an angular node - in this case the plane containing the nucleus and bisecting the two lobes of the p orbital. There are two different 3d orbitals depicted - both have two angular nodes and zero radial nodes.

Predicting electron configurations for many electron atoms

In generating the ground state electron configuration for an atom, three simple rules must be applied:

Pauli exclusion principle. The principle states that no two electrons in an atom can have the same set of values for the four quantum numbers n, l, m_l , and m_s. What this means is that no more than two electrons can be accommodated in an orbital, and the two electrons in a filled orbital must have their spins paired (one electron with m_s =  + ½ , the other with m_s =  − ½ ).

The aufbau principle (Aufbau = "building-up" in German). Each electron is to be added to the unfilled orbital with the lowest energy. This means we start adding electrons at the bottom of the energy level diagram above, and work our way up. We can think of the aufbau principle as consistent with the idea that systems tend to spontaneously adopt a minimum in energy. The electron configurations we are building up are ground state configurations - they are the lowest possible energy of the system consisting of the nucleus and however many electrons needed to make up the atom (or ion) under consideration.

Hund's rule. In case of degenerate orbitals (orbitals of equal energy, as in subshells with multiple orbitals), electrons should be placed in an empty orbital, with a second electron to be added to a singly occupied orbital only after all of the degenerate orbitals already have an electron. The reason for this rule is that electrons in different orbitals of a subshell - for example 2p_x and 2p_y - occupy different regions of space and therefore repel each other less than if they were both in the same orbital. The former situation is of lower energy and so is a more stable electron configuration.

Building up electron configurations - an example

Let us use our orbital energy level diagram to predict the electron configuration of sulfur. The atomic number of sulfur is 16, so there will be 16 electrons in a neutral sulfur atom. We start filling in electrons in our diagram (refer to the figure below, panel (i)) according to the aufbau principle, starting with the lowest energy orbital. By the Pauli exclusion principle, each orbital will accommodate two electrons, with spins paired (one up, one down). The first two electrons are placed in the 1s orbital, which fills the lowest energy first shell. The next eight electrons are enough to fill completely the second shell (consisting of the single 2s orbital plus the three 2p orbitals). Thus, the first two shells are filled completely with 10 electrons, yielding a set of what we will call core electrons, corresponding to the electron configuration of neon [Ne]. The remaining six electrons (panel (ii) below) are not enough to fill the third shell (since, like the second shell, it can hold eight electrons), so they are denoted as valence electrons, which we define in general as the electrons in an outermost, unfilled shell of an atom. So for this example, the third shell is the valence shell, the shell that contains the outermost, or valence electrons. To complete the electron configuration, we again follow the aufbau principle by filling the 3s subshell with two electrons, leaving four (panel (iii) below). Hund's rule comes into play next, since the subshell contains three orbitals, by definition equal in energy. Hund's rule tells us to place one electron in each unoccupied orbital (panel (iv)), pairing electrons in these orbitals only after each orbital has one electron. Panel (v) below shows the finished electron configuration, after we have placed the last remaining electron in one of the singly-occupied orbitals of the 3p subshell.

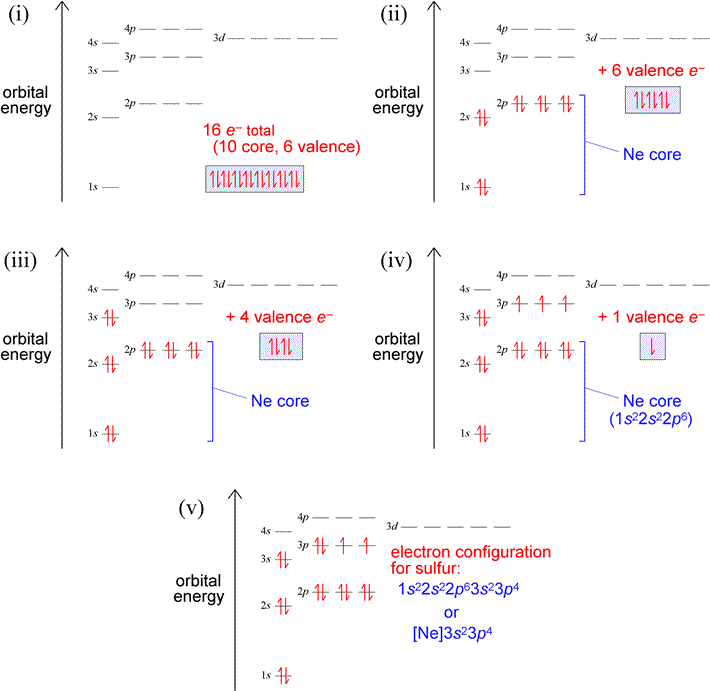
Exercises: (a) Which elements have the electron configurations depicted in panels (iii) and (iv) in the figure above? Write out the electron configurations in the single-line format for the atoms of both these elements. (b) Build up the electron configuration for oxygen (Z = 8), and compare with that of sulfur. How are the two electron configurations similar? Locate the two elements in the periodic table. Does this suggest a general principle about electron figurations and groups in the periodic table?