Lecture 25. Acid-base equilibria II
Thursday 25 April 2024
Case study: Weak acid dissociation equilibrium. The acid dissociation equation and Ka, the acid dissociation constant. Strong and weak acid pH calculations. Base hydrolysis and the definition of Kb. Strong and weak base pH calculations.
Reading: Tro NJ. Chemistry: Structure and Properties (3rd ed.) - Ch.16 §16.1 - §16.7 (pp.713-734b)
Summary II
As we finish our semester-long study of chemistry, let us apply our understanding of chemical equilibria to a very important category of reactions, those of acids and bases. We have learned a general definition of acids and bases according to Brønsted-Lowry, and developed a set of relationships based upon the defintion of pH and the autoinonization of water and the definition of Kw and we shall employ these, along with our toolkit of writing equilibrium constant expressions given a chemical equation, interpreting the magnitude of equilibrium constants, and using the ICE table method as a foundation for accomplishing our objectives. We'll first need to introduce some notation and defintions specific to acid-base chemistry. These are the general chemical equations for an acid dissociation reaction and the similar but distinct base hydrolysis reaction. Their corresponding equilibrium constants are labeled as Ka and Kb.
The acid dissociation equation and Ka
The acid dissociation equation for a general acid HA
HA = H+ + A−
is defining for the acid dissociation constant, Ka:
Ka = [H+][A– ] / [HA]
Ka provides a quantitative measure of acid strength. For strong acids, Ka is very large (Ka >> 1). This also means that a strong acid is also a strong electrolyte, since its dissociation in water creates the charged species hydronium ion, H3O+(aq). A weak acid (Ka << 1) remains largely undissociated, creating only small concentrations of hydronium in water, making weak acids weak electrolytes.
The base hydrolysis equation and the definition of Kb
Kb is known as the base hydrolysis constant, or simply "base constant". It is defined by the chemical equation for abstraction by a base of a proton from water, called the base hydrolysis equation.
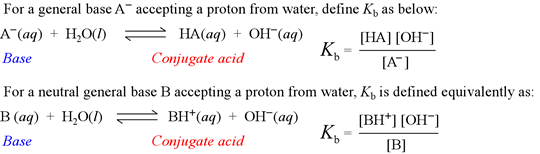
Note that the base hydrolysis equation is a complete Brønsted-Lowry acid-base reaction, with water as the reactant acid. The expression for the base constant is derived by following the usual rules for writing an equilibrium constant for a chemical reaction, with the additional feature that the concentration of water is dropped from the expression. This is because in dilute aqueous solution, the concentration of water remains practically constant.
Since the for any acidic or basic substance in water, the equilibrium for the autoionization of water must still be satisfied, we ought to be able to show that for any Brønsted-Lowry conjugate pair, Kb· Kb = Kw. In other words, the equilibrium relations are not independent!
The quantitative treatment of weak acid and weak base equilibria can be found here.