GENERAL CHEMISTRY TOPICS
Acids and bases: The Brønsted-Lowry definition
Acids and bases: The Brønsted-Lowry definition. Conjugate acid-base pairs. Reciprocal strength relationship. Water as base and an acid. Autodissociation of water. Strengths of acids and bases. Definition of Ka, the acid dissociation constant, and pKa. Definition of Kb and pKb. Relationship between Ka, Kb, and Kw.
To advance our treatment of acid-base chemistry, we'll employ the Brønsted-Lowry definitions of acids and bases. (Often we will lapse into referring to the Brønsted-Lowry definition as the "Brønsted" definition, or speak of "Brønsted acids" or "Brønsted bases".) The Brønsted-Lowry definition simply states that an acid is a proton (H+) donor, and a base is a proton acceptor. The Brønsted-Lowry definition is quite general, and it is important to note that among both acids and bases are molecules, anions, and cations, and furthermore there are some species capable of acting as either a Brønsted-Lowry acid or a Brønsted-Lowry base. As we shall see, water is an example of a species that can act as an acid or a base according to the Brønsted-Lowry definition.
A Brønsted-Lowry acid must contain at least one hydrogen atom, typically attached to a very electronegative atom such as oxygen. When a Brønsted-Lowry acid donates (gives up) a proton, it loses one H from its formula, and its charge decreases by one. The resulting species is by definition a base, since a reversal of the loss of the proton is a gain of a proton, and the species gaining the proton is acting as a proton acceptor. It is convenient to write equations that represent Brønsted-Lowry acids losing a proton. We will refer to such an equation as an acid dissociation equation. We will often represent the acid dissociation equation in a general form. In the following acid dissociation equation, HA is the generalized Brønsted-Lowry acid.
HA = H+ + A−
Note that the species that results from the acid when it dissociates according to this equation has one less hydrogen in its formula, and its charge is one less. The species A− that arises from dissociation of a proton from the acid HA is capable of acting as a base, according to the reverse of the acid dissociation equation. When the Brønsted-Lowry base accepts a proton, it becomes HA, a Brønsted-Lowry acid. We thus refer to A− as the conjugate base of the acid HA. We can just as well refer to HA as the conjugate acid of the Brønsted-Lowry base A−. This concept of conjugate acid-base pairs is a key point of the Brønsted-Lowry description of acids and bases that must be mastered in order to progress in our understanding of acid-base chemistry within the Brønsted-Lowry framework.
In introducing the Brønsted-Lowry formalism via the acid dissociation equation, we make an analogy to redox reactions that will help clarify the basic concepts and assist us in applying them to the great variety of acid-base reactions we may encounter. Just as in redox reactions, where an oxidation always occurs in concert with a reduction, so too in acid-base reactions there is always one species that acts as the Brønsted-Lowry acid and another that acts as the Brønsted-Lowry base. These are not the conjugate pairs we just defined. A complete Brønsted-Lowry acid base reaction consists of two conjugate acid-base pairs. Note that in the acid dissociation equation above, the proton lost by the acid HA appears on the product side, but we have not specified what species gains (accepts) the proton. That is, the acid dissociation equation does not include a Brønsted-Lowry base as a reactant. Thus, we think of the acid dissociation equation of a half-reaction, which must be combined with another acid dissociation equation to form the chemical equation for a complete Brønsted-Lowry acid-base reaction. The recipe for this is that one of the acid dissociation equations must be written in reverse, and added to the other acid dissociation equation. Note that if we had written H+(aq) as the product of acid dissociation of HA, this represents the transfer of H+ to water, acting as a base. Recall that H+(aq) is an abbreviation for H3O+(aq) and other species that represent proton transferred to water. The complete Brønsted-Lowry acid-base reaction for a general Brønsted-Lowry acid HA reacting with water - the latter acting as a Brønsted-Lowry base - is shown below.
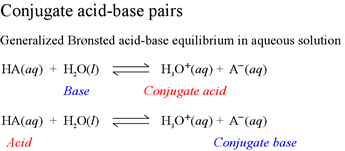
Note how two conjugate acid-base pairs are involved in this complete Brønsted-Lowry acid-base reaction involving the reactants HA, a general Brønsted-Lowry acid, and water, acting as a Brønsted-Lowry base. Note how the acids and bases that "go together" as conjugate pairs are identified in this equation. Hydronium ion is the conjugate acid of water (as a base), while A− is the conjugate base of the acid HA.
The reaction as written is the combination of the following two acid dissociation reactions.
HA = H+ + A−
H3O+ = H+ + H2O.
The first equation is kept as is (written as an acid dissociation), while the second is reversed (written as a base accepting a proton), then the two equations are added together.
Reciprocal strength relationship
Every Brønsted-Lowry acid has a conjugate base, as the acid dissociation equation shows. When we say an acid is a strong acid, we mean that it has a strong tendency to transfer a proton. Conversely, once a strong acid has lost a proton, it is now the conjugate base, and if the acid that gave rise to it readily loses its proton (i.e. the acid is strong), then the conjugate base is necessarily a weak base, showing little tendency to reform the strong acid by accepting a proton. This reciprocal strength relationship is simply a consequence of the Brønsted-Lowry definition and its view of acids and bases existing as conjugate pairs.
But to say an acid is a strong acid actually implies a comparison with other acids. If a particular acid is to act as an acid, there must be a base - the conjugate base of a different acid - to accept the proton. If HA is a stronger acid than HB, then HA has a stronger tendency to donate a proton than HB. Because of the reciprocal strength relationship between any Brønsted-Lowry acid and its conjugate base, A− is a weaker base than B−. This means that in a complete acid base reaction, the stronger acid HA and the stronger base B− will be converted to the weaker acid HB and the weaker base A−. In other words, in a reaction involving two conjugate pairs, the equilibrium will favor the weaker acid and weaker base. We will see how to make this qualitative statement a quantitative relationship.
Water as base and an acid
We have seen above an example of water reacting as a Brønsted-Lowry base with a general Brønsted-Lowry acid HA. We can also write a chemical equation for water acting as a Brønsted-Lowry acid reacting with a general Brønsted-Lowry base. Below, we write both of these equations next to one another for comparison. Apparently, water can act as either a Brønsted-Lowry base or a Brønsted-Lowry acid.
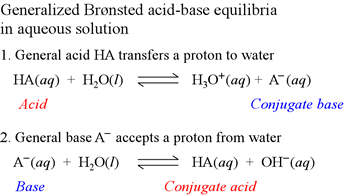
Note that in the first equation, the acid HA transfers a proton to water (water is acting as a base here), producing the conjugate base of HA, A−, and the conjugate acid of water, hydronium ion, H3O+. In the second equation, the base A− reacts with water (water is acting as an acid here), producing the conjugate acid of A−, HA, and OH−, the conjugate base of water.
Substances - like water - that can act as both an acid and a base are termed amphiprotic. Examples of other amphiprotic species are the following:
Hydrogen carbonate (bicarbonate): HCO3−
Hydrogen sulfate (bisulfate): HSO4−
Hydrogen phosphate: HPO42− ; Dihydrogen phosphate: H2PO4− .
Exercise: For each of the species above, deduce the formula for its conjugate acid and conjugate base, and write an acid dissociation equation including the species as an acid and an acid dissociation equation including the species as a base. You will have eight acid dissociation equations in all.
Autodissociation of water
Now that we have noted how water can play the role of a Brønsted-Lowry acid or that of a Brønsted-Lowry base, we are prepared to see how both roles of water can be combined into a single equation representing a complete Brønsted-Lowry acid-base reaction. The reaction, shown below, is the so-called autodissociation of water. (Note that in some sources, this is called autoprotolysis, or autoionization.
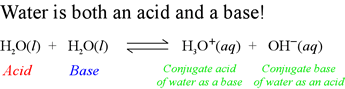
This reaction is the combination of two acid dissociation equations (half-reactions):
H2O = H+ + OH − (Water
as an acid)
H3O+ = H+ + H2O
(Hydronium ion as an acid; water is the conjugate base.)
The above reaction is the sum of the first acid dissociation reaction at right, and the reverse of the second.
It turns out that water is quite a weak acid and also quite weak as a base, hence the weaker acid-base pair is on the left-hand side (reactant side) of the above autodissociation equation. The reciprocal strength relationship tells us that hydronium ion is a strong acid and that hydroxide ion is a strong base. Furthermore, we can deduce that the equilibrium lies very far to the left, greatly favoring the reactant, water. Therefore, only a very small amount of water is dissociated at equilibrium and water itself is classified as a nonelectrolyte.
We can quantify water's small tendency to autodissociate by defining a special type of equilibrium constant called Kw and assigning an experimentally determined value to it.
Kw = [ H+ ][ OH − ] = 1.0 × 10−14 (at 25°C).
Note that this is the equilibrium constant expression that we would write for the chemical equation representing the autodissociation reaction of water, considering the concentration of water as a constant. The very small value for Kw reflects the very weak propensity of water to autodissociate.
Strengths of acids and bases
In our study of acids and bases we will consider almost exclusively aqueous solutions of acids and bases. So the strength of water itself as an acid or as a base will provide the most relevant reference for strengths of acids and bases. A broad, but useful, generalization will be to consider hydronium ion and any acid stronger than hydronium ion a strong acid in water. We will consider acids weaker than hydronium ion to be weak acids. Similarly, we will consider the hydroxide ion and any base stronger than hydroxide ion strong bases, and any base weaker than hydroxide to be a weak base in water.
In order to measure the strengths of acids and bases quantitative, we'll need to define the quantities Ka and Kb, the acid dissociation constant, and the base hydrolysis constant, respectively. Like Kw, Ka and Kb are special forms of the equilibrium constant that apply to acid-base chemical equations. Having defined these three constants, we can easily derive an equation that relates them and is a quantitative statement of the reciprocal strength relationship.
Definition of Ka, the acid dissociation constant, and pKa
For the general acid dissociation equation,
HA = H+ + A–
we define Ka, the acid dissociation constant, by forming the expression
Ka = [H+][A– ] / [HA].
Note how we apply the normal rules for writing an equilibrium constant - concentrations of products in the numerator, concentrations of reactants in the denominator - to the acid dissociation equation in defining Ka.
By analogy to the definition of pH, we define pKa as
pKa = − log Ka = − log {[H+][A− ] / [HA]}.
We will use Ka and pKa as a quantitative measures of acid strength. A quantitative treatment of weak acid and weak base equilibria can be referenced here.
Definition of Kb and pKb
Kb is known as the base hydrolysis constant, or simply "base constant". It is defined by the chemical equation for abstraction by a base of a proton from water, called the base hydrolysis equation.
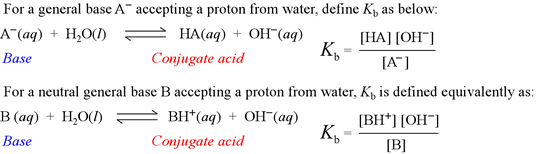
Note that the base hydrolysis equation is a complete Brønsted-Lowry acid-base reaction, with water as the reactant acid. The expression for the base constant is derived by following the usual rules for writing an equilibrium constant for a chemical reaction, with the additional feature that the concentration of water is dropped from the expression. This is because in dilute aqueous solution, the concentration of water remains practically constant.
By analogy to the definition of pH, we define pKb as
pKb = – log Kb
We will use Kb and pKb as a quantitative measures of base strength.
Relationship between Ka, Kb, and Kw
If we combine the general equations defining Ka and Kb, and use the rule for combining equilibrium constants when reactions are summed (the equilibrium constants are multiplied), we obtain a simple and useful relationship between Ka, Kb, and Kw:
HA = H+ + A– Ka = [H+][A– ] / [HA].
A– + H2O = HA + OH – . Kb = [HA][OH –] / [A–].
sum: H2O = H+ + OH – Keq = Ka· Kb = [H+][OH– ] = Kw.
We have derived the relation Kw = Ka· Kb, which hold for aqueous solutions of acids and bases. The logarithmic form of the relation is pKw = pKa + pKb. When the temperature is 25°C, Kw. = 1.0 x 10–14, so that
Ka· Kb = 1.0 x 10–14 (at 25°C), and
pKa + pKb = 14.00 (at 25°C).
The values Ka and pKa are measures of how strong an acid is.
The higher the Ka, the stronger the acid. Since
pKa = – logKa,
the lower pKa as, the stronger the acid.
If we want to compare different bases in terms of their strength as bases,
we can use the Kb, or pKb values.
The greater a base's Kb (or lower its pKb),
the stronger the base. Remember, as the strength of an acid decreases,
its conjugate base increases in base strength, and vice-versa.
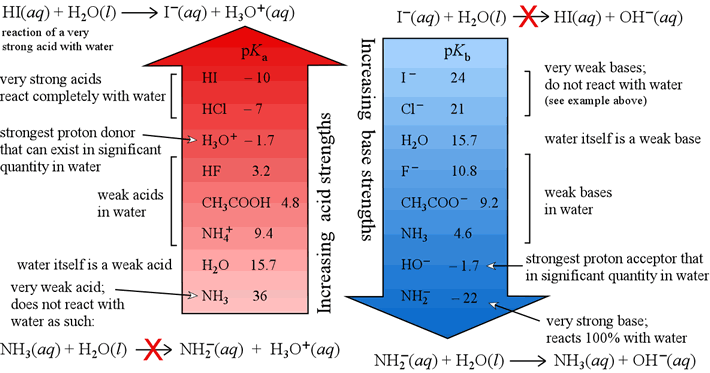
The figure below shows a comparative scale of acid strength of some acids (on the left) and, on the right, a comparative scale of base strength of the conjugate bases of those acids.