GENERAL CHEMISTRY TOPICS

Calorimetry

Measuring heat. Constant pressure calorimetry. Constant volume, or "bomb" calorimetry.

---

The measurement of of the energy produced or consumed in processes is termed calorimetry. The definition of specific heat capacity (sometimes referred to simply as specific heat) entails a very important relation for calorimetry. It states that the product of the mass of a system and its specific heat capacity is the direct proportionality factor that multiples the value of the change in temperature (ΔT) to give the corresponding quantity of energy transfered as heat.

This equation states that the energy gained or lost by a system as heat is given by the mass times specific heat capacity times the change in temperature ΔT that occurs. In calorimetry, we'll determine q by measuring ΔT for a process within a system.

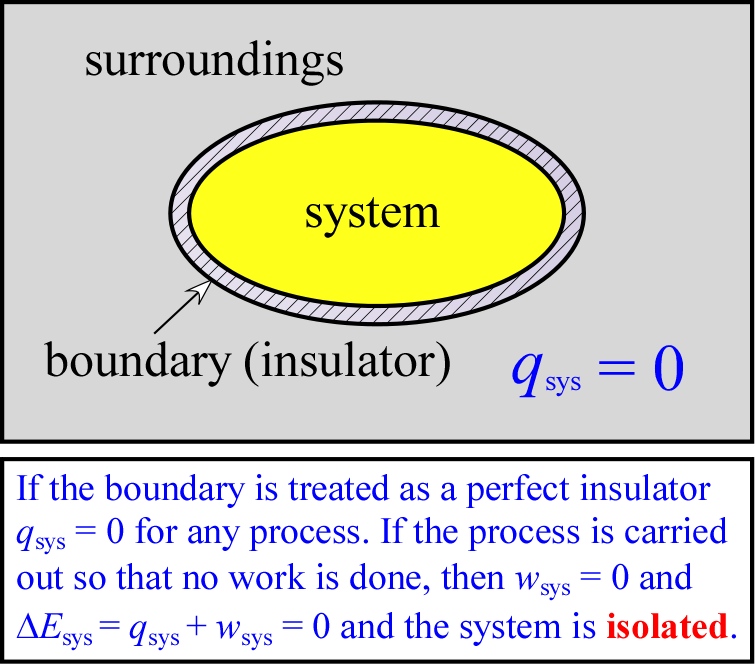
In practice, calorimetry depends on the use of an experimental system that approximates what is termed an isolated system, one that permits no exchange of matter or energy with its surroundings. Such as system is at the heart of what is called a calorimeter. The figure at right illustrates abstractly the concept of an isolated system. A system that permits no exchange of matter with the surroundings (but could exchange energy with its surroundings) is termed a closed system. Thus, an isolated system is a closed system that also cannot exchange energy with its surroundings. Since energy exchanges are accounted for by heat (q) transferred to or from the system (thus gained or lost by the surroundings) and work (w) performed by or on the system (entailing energy gained or lost by the surroundings), we can express the requirements for an isolated system as q_sys = 0 and w_sys = 0.

The foregoing is closely related to the first law of thermodynamics. This is because heat q and work w are regarded as the only contributions to energy exchanges between a system and its surroundings. Therefore ΔE_sys = 0 for an isolated system. Again from a practical standpoint, it is much easier to construct a system that is effectively closed - any system bounded completely by an impenetrable physical barrier would suffice. Furthermore, if we limit the possible contribution of work to mechanical work of the form of expansion or contraction of the system (volume changes of the system) relative to an external pressure, we can keep w_sys = 0 by having our system boundary fixed (i.e. ΔV_sys = 0). However, there is no such thing as a perfect insulator, meaning that if there is a temperature difference between system and surroundings, q_sys ≠ 0, although the rate of heat energy transfer might be exceedingly slow. But the requirement for calorimetry need only be an approximation of an isolated system, such as would be constituted by a tightly closed thermos bottle. For such a system, q_sys ≈ 0 over a time interval sufficient to complete experimental measurements. Corrections can also be made for a slow rate of heat exchange between the calorimeter and its surroundings.

It is also very important to note that application of the first law of thermodynamics to this example yields the following relations:

ΔE  =  q_sys  +  w_sys  =  0    (since the system is isolated)

q_sys =  0   and  w_sys  =  0    (since the system is isolated)

q_sys =  q₁  +  q₂  =  0

q₁ =  − q₂   (q₁ > 0;  q₂ < 0)

We can apply these basic concepts to the measurement of the energy produced or consumed in the form of heat q for various processes, such as phase changes, formation of solutions, and chemical reactions.

We'll assume here the relevant specific heat capacity values are given (units J g⁻¹ °C⁻¹) and used in the above equation to calculate q from measured values of m and ΔT. These definitions are shown in the adjacent figure.

Let's suppose now that we want to measure q_rxn for a chemical reaction occurring between species in aqueous solution. In this case, the solute reactant species and the products are only a small portion of the mass of the system, which is mostly solvent (water). We can readily perform the reaction in the lab by mixing two reactant solutions. Any heat released or absorbed by the reaction will affect the whole solution (the whole system). As our measurement of this heat of reaction will be more accurate if the system is isolated, the vessel into which we mix reactant solutions should be insulated. A styrofoam coffee cup "calorimeter" actually approximates an isolated system well enough, plus we are able to make small corrections for the slow rate of heat transfer between system and surroundings.

Since the reactants are solute species, and thus part of the system, we find it convenient to take a similar view of the system as in the introductory heat transfer example, and treat the system as a composite. There is no actual boundary between reactants and the bulk of the solution, so this is a purely conceptual "boundary". But this allows us to write

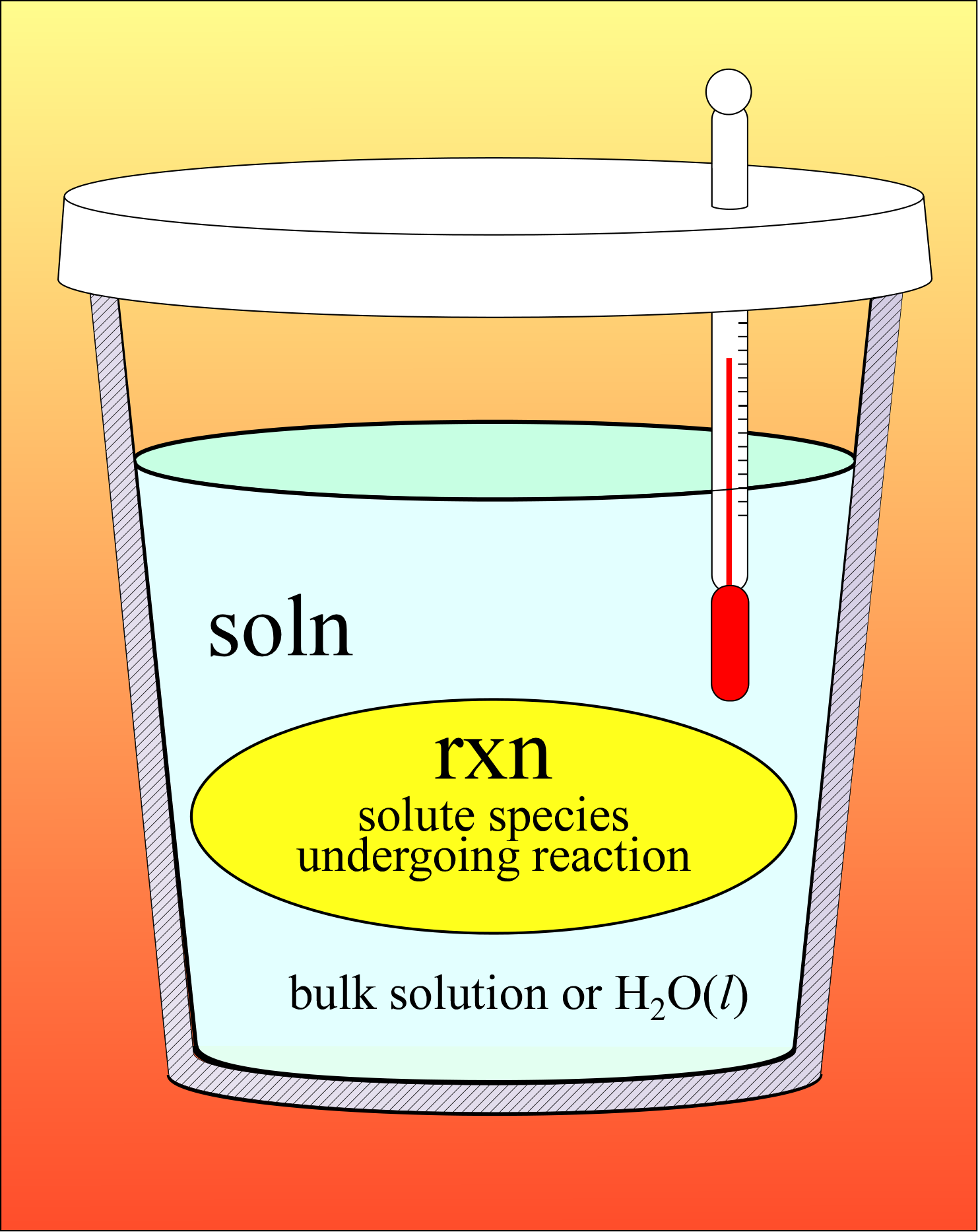
q_sys =  0         (since the system is isolated)

q_sys =  q_rxn  +  q_soln  =  0

q_rxn =  − q_soln

Since we will measure the temperature change for the the system as a whole, that is the whole solution contained within the coffee cup calorimeter, the equation for q is applied to the solution:

q_rxn =  − q_soln  =  − m_soln × c_{s, soln} × ΔT_soln

Our coffee cup calorimeter is not truly an isolated system, but will suffice as a good enough approximation. Another feature of the system is that the pressure to which it is exposed is the ambient atmospheric pressure, which we will take to be constant, so the the heat that is measured is under constant pressure conditions. This makes it a measure of the bulk enthalpy change (extensive) associated with the particular amount of reactants converted to products. The enthalpy of reaction is an intensive quantity that is obtained by dividing the extensive heat of reaction measured by the appropriate chemical amount (mol_rxn) of reactant species.

ΔH_{total, rxn} =  q_rxn       (extensive)

ΔH_rxn =  q_rxn / n       (n mol_rxn, intensive)

Let's illustrate the approach described above with a concrete example.

Neutralization reaction example

Example: Sodium hydroxide reacts with hydrochloric acid according to the following chemical equation

NaOH(aq) + HCl(aq)   →   NaCl(aq) + H₂O(l)

When 25.00 mL of 1.120 M NaOH(aq) and 25.00 mL of 1.050 M HCl(aq), both at an initial temperature of at 20.30 °C are mixed, the resulting temperature of the solution that forms is 27.30 °C. Find the ΔH_rxn, the reaction enthalpy, in units kJ/mol for the reaction as written.

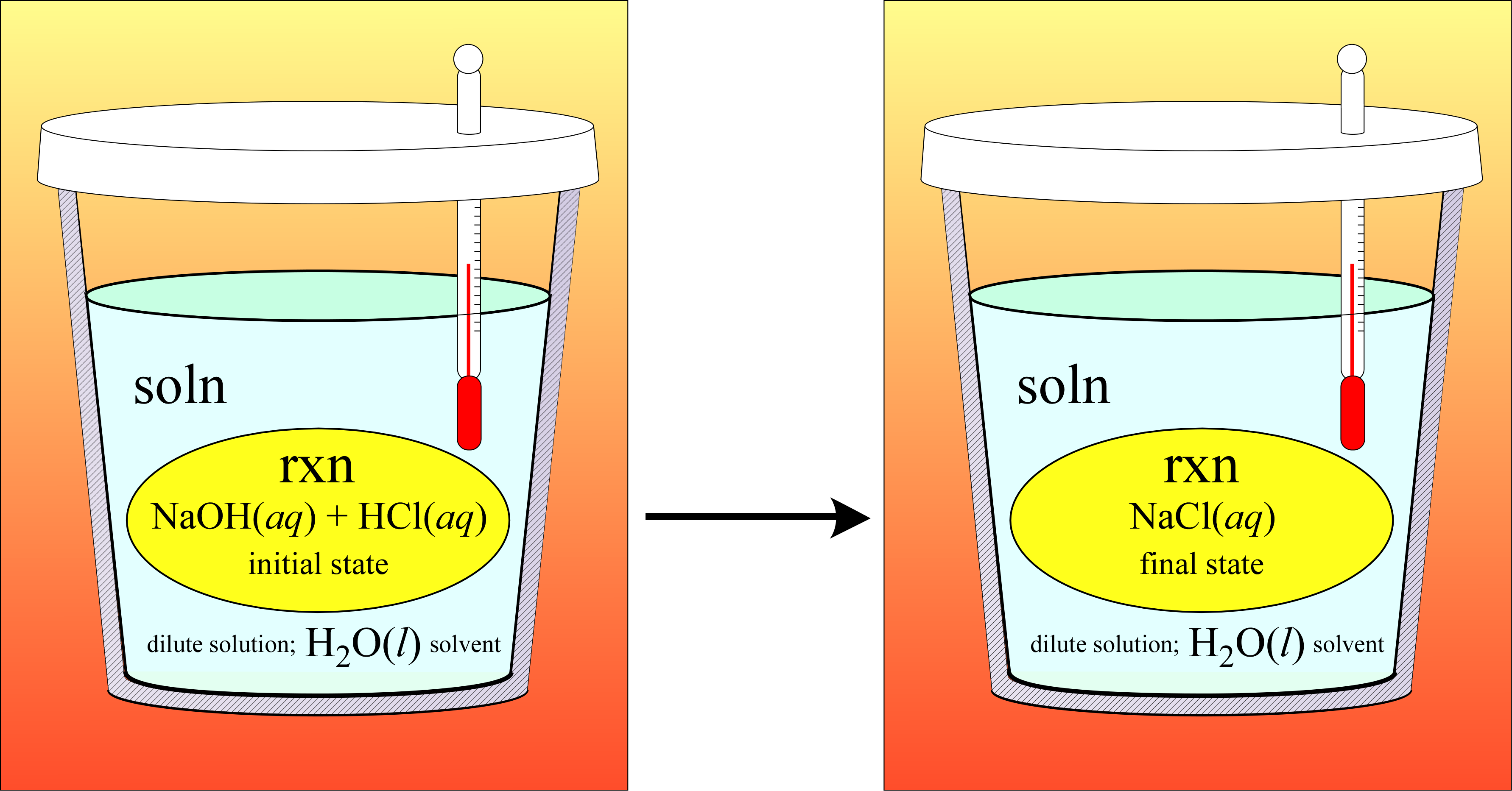
Our general strategy will be to calculate q_soln which we take to be equal to −q_rxn under the assumption that the system consisting of the entire solution (bulk solution plus reacting species) is isolated. To finish, we divide by the chemical amount of reaction (mol_rxn)

 

Setting up the calculation of q_soln,

q_soln = m_soln × c_{s, soln} × ΔT_soln

q_soln = (50.00 g)(4.184 J/g·°C)(7.00 °C)

q_soln = 1464.4 J = 1.64 kJ (3 s.f.)

This represents the bulk (extensive) enthalpy change of the solution, which we take here to be the surroundings to which the system of reactants is exchanging energy as heat at constant pressure. Treating the solution in entirety as an isolated system, we can conclude

q_rxn   =   −q_soln

Note that q_rxn < 0. The release of energy from the reaction, raising the temperature of the solution, makes it an exothermic reaction.

The next step to obtain the intensive quantity ΔH_rxn. Let's look again at the chemical equation for the neutralization reaction. A complete ionic equation representation for this would reduce to the general net ionic equation for a neutralization reaction between a strong acid and a strong base in aqueous solution.

H⁺(aq) + OH⁻(aq)   →   H₂O(l)

The stoichiometry of the reaction is quite simple, with all leading coefficients equal to one. The mol amount that reacts in this example will be then determined by the limiting reactant, either H⁺ or OH⁻, whichever is less. We obtain these amounts from the given volumes and concentrations of the solutions that are mixed to produce the reaction.

mol H⁺(aq)   =   V_HCl × c_HCl

mol H⁺(aq)   =   (0.02500 L)(1.050 M)   =   2.625 × 10⁻² mol H⁺

mol OH⁻(aq)   =   V_NaOH × c_NaOH

mol OH⁻(aq)   =   (0.02500 L)(1.120 M)   =   2.800 × 10⁻² mol OH⁻

Since the chemical amount (mol) of is less, it is the limiting reactant and serves here as the value of n mol_rxn:

ΔH_rxn   =   −q_soln / n

ΔH_rxn   = −1.4644 kJ / 2.625 × 10⁻² mol

ΔH_rxn   = −55.8 kJ / mol

The result here is reported to three significant figures because the input value for q_soln is limited to that precision.

Energy change associated with a process: Phase change example

An energy transfer process can occur with heat q ≠ 0 but with ΔT = 0! In other words, there can be thermal energy exchange without a temperature change. Let us analyze the energetics of a simple phase change example. Our system is an ice cube of mass 18 g at exactly 0 °C. Let us assume that the surroundings are slightly warmer, so that spontaneous energy transfer occurs.

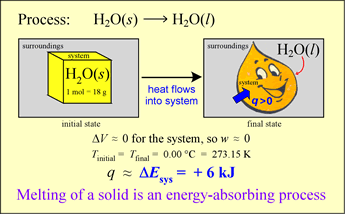
The system will increase in energy as a result since q > 0 and (for reasons that will be evident shortly) the work done on or by the system is negligible. Thus

         ΔE ≈ q < 0  

What happens under these circumstances? The ice melts, gradually it is all converted to liquid water. At the same time, it is observed that the temperature of the system remains constant as long as some of the ice remains. Where does the energy q go if ΔT = 0?

The answer is that there is an energy requirement for the phase change, an input to the system equivalent to the so-called molar heat of fusion. The water molecules in ice are all in hydrogen bond interactions with each other, a particularly strong type of intermolecular attractive force, and the fully-hydrogen bonded water molecules of ice are thereby locked into an ordered lattice that gives the ice cube the shape and solidity characteristic of the solid phase. Some of these hydrogen bond interactions must be broken so that the water molecules can acquire the freedom of motion characteristic of the liquid phase. Virtually all the energy the ice cube system acquires from the surroundings must go into giving the water molecules sufficient kinetic energy to break and loosen enough of the hydrogen bonds to accomplish the complete phase transition. Once all of the ice is converted to water, the further input of energy q from the surroundings would begin to raise the temperature of the liquid water.