GENERAL CHEMISTRY TOPICS
Ionization energy
Definition and chemical equation for ionization energy (IE). Periodic trends in IE.
The ionization energy (IE) of an atom of element X is the energy associated with the process (represented in the following chemical equation):
X(g) → X+(g) + e–
The ionization energy is the change in energy for this process, or the difference in energy between the ionized products (on the right) and the starting, or initial state of X in the gas phase (on the left). This energy must be positive, due to the law of electrostatic attraction. It requires an input of energy to cause the ionization of any element X. For the hydrogen atom, we can calculate the ionization energy by setting the energy of the reference (zero) of electrostatic potential energy to that of the ionized products completely separated (r = ∞ in Coulomb's law), minus the energy of the electron in the ground state (n = 1):
IE = 0 − (−2.18 × 10−18 J / n2 )
IE = + 2.18 × 10−18 J (n = 1)
We convert this energy on the atomic scale to a macroscopic energy unit by using Avogadro's number. For the hydrogen atom example,
IE = (+ 2.18 × 10−18 J )(10−3 kJ/J)(6.022 × 1023 mol−1 ) = 1.31 × 102 kJ·mol−1
The first equation above represents the first ionization energy (IE1) of X. The second ionization energy (IE2) would be represented as
X+(g) → X2+(g) + e–
Third ionization energies, and so on, are similarly definable. While it should be clear that for any given element IE1 < IE2 < IE3, there are clear periodic trends in the various ionization energies. These are explained by the electron configurations of the elements.
Trends in ionization energy
The lowest ionization energies occur for metals, and the highest ionization energies are seen with noble gases (Group 8A).
The pattern of ionization energies for the elements reflect a distinction between valence and core electrons.
A plot of first ionization energies (IE1) for elements 1-20 shows the general trend of increasing from left to right across a period (as Zeff increases) and decreasing from top to bottom (as principal quantum number n increases and Zeff `remains about the same).
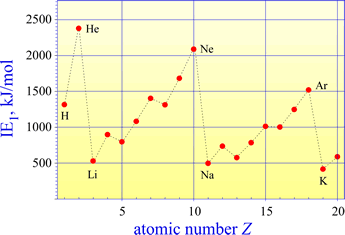
The highest IE1 values are seen for the noble gases (He, Ne, Ar). This is because a maximum of Zeff in the period is reached and the valence shell is filled. The Group 1A elements have the lowest IE1 values, as Zeff is at a minimum value and a single valence electron occupies the "new", larger valence shell.
The graph of first ionization energies for elements 1-20 shows two exceptions to the general trend of increasing from left to right across periods 2 and 3. A decrease in IE1 is seen from Group 2A to Group 3A, and from Group 5A to 6A. The energy level diagrams for the valence electrons of period 2 elements shown below will aid us in explaining these exceptions.
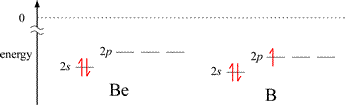
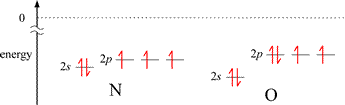
The first exception, illustrated by the decrease in IE1 for B compared to the preceding 2nd period element Be, can be explained readily by the energy difference between a valence electron in ns and the np orbitals for a given n. The valence electron in the 2p orbital of boron is higher in energy than the lowest energy valence electron in beryllium (occupying a 2s orbital), and the difference in energy is less for the 2p electron in B to reach ionization (the zero reference shown by the dotted line), even though the energies of the corresponding 2s and 2p orbitals in B are slightly lower in B compared to Be. The situation is a little more nuanced for the second case. The nitrogen atom has a half-filled subshell: none of the 2p valence electrons is paired. Pairing the first unpaired electron to form the oxygen electron configuration results in extra destabilization (increased energy) because of electron-electron repulsion due to the doubly-occupied 2p orbital.