GENERAL CHEMISTRY TOPICS

Significant figures

Counting significant figures ("sig-figs"). Degree of precision. Treating exact numbers and sig-figs in calculations. Roundoff error: What it is and how to avoid it. Unit equivalence relations and conversion factors.

---

The concept of significant figures ("sig-figs") and how to properly treat them in calculations is important in any experimental science. In any measurement, there is a degree of uncertainty, and the values reported from a measurement ought to reflect that uncertainty. So for the example of a buret reading, we make our best estimate of the actual reading and we also note the estimated uncertainty in the last place digit.

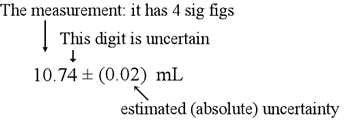
Of course, when we perform a measurement, we ought to be well aware of the uncertainty and the correct number of digits to report. In cases where a number is given that is supposed to be the result of of some measurement, how should significant figures be counted in general? The following rules are used to assess significant figures.

Counting significant figures

1. Count all non-zero digits
2. Count zeros that occur in between non-zero digits
3. Leading zeros (e.g. zeros written to the right of the decimal point before the first non-zero digit) are not significant. For instance, 0.008206 has four significant figures.
4. Trailing zeros are significant if they are to the right of the decimal point. For instance, 273.00 has five significant figures. Trailing zeros to the left of a decimal point are also significant, but if there is no decimal point (e.g. the number 45,000) the trailing zeros could be non-significant. Best practice is to use scientific notation to represent significant figures,which avoids any ambiguity - 45,000 may represent 4.5 × 10³ (2 significant figures), or 4.5000 × 10³ (5 significant figures).

Degree of precision

Degree of precision is simply a term for the number of significant figures to the right of the decimal point in a given representation of a number. The type of measurement providing such a number gives rise to a corresponding expression of degree of precision. For example, a common laboratory operation is obtaining a mass of a sample from a preparatory pan balance, which provides a digital readout of a number (e.g. 86.412) with a degree of precision of three, corresponding to a measurement in grams, precise to the nearest 0.001 g (thousandth of a gram), or to the nearest milligram.

Rules for significant figures in calculations

Here is a summary of "rules of thumb" for determining the proper number of significant figures to report in the results of a calculation:

(1) Addition and subtraction: Express all numbers in scientific notation and with the same exponent (power of ten). Arrange the numbers with the decimal points lined up, just as is normally done in adding and subtracting numbers by hand. The significant figures of the result is determined by the last digit which is furthest to the left. In other words, the number of digits to the right of the decimal point - what was defined above as degree of precision - in the result should be equal to the number of digits to the right of the decimal point in the quantity with the fewest such digits. Succinctly stated, the degree of precision of the result is determined by the smallest degree of precision of the input.

(2) Multiplication and division: This is the simplest rule to put into words. The significant figures of the result is determined by how many sig figs the number with the fewest sig figs in the calculation has. In other words, the number with the fewest sig figs limits the sig figs of the result.

Example: In parts (a)-(d), a calculator operation and its result are presented. How would you express each answer with the correct number of significant figures?

(a) 3.512 + 1.77 = 5.282
(b) 12.3 − 2.82 = 44.68
(c) 1.48 × 8.4 = 12.432
(d) 0.00286 ÷ 4.184 × 10⁻³ = 0.683556405

Roundoff error: What it is and how to avoid it

Let us illustrate the pitfall of roundoff error and the proper way to perform calculations that require two or more operations by means of an example.

Example: A student performs a calculation for a calorimetry lab exercise based on the following data. The dissolution of 4.120 g of a substance S having a formula mass of 80.05 g/mol resulted in the production of 1.078 kJ of heat energy. In calculating the molar heat of dissolution of S, which should yield a number with the units kJ/mol, the student did the following:

(4.120 g S) / (80.05 g S/mol S)   =  0.051 mol S 

 (1.078 kJ) / (0.051 mol S)  =  21.14 kJ/mol S

What is wrong with this calculation, and what is the correct answer?

Analysis: Note that the form of the calculation is correct; dimensional analysis (see below) shows that the input units cancel correctly to yield the correct units. This is good. Also correct is the reporting of the final answer with four significant figures. However, the error lies in improper rounding of the result of the first step. The calculation, if performed in a single step or sequentially using a calculator, and then rounding to the correct number of significant figures (according to rule (2) above) would yield

 (1.078 kJ)(80.05 g S/mol S) / (4.120 g S) = 20.95 kJ/mol S

If one performed two separate steps in such a calculation, the result of the first step needs to be fed into the next step with at least one more figure than the number of significant figures, then rounding the final result:

(4.120 g S) / (80.05 g S/mol S)   =  0.051468 mol

(1.078 kJ) / (0.051468 mol S)  =  20.945 kJ/mol S

→   round to 20.95 kJ/mol S

Although the student performed well in the lab exercise, one point was deducted from the student's grade because roundoff error was introduced into the calculation.

(Note: See also the discussion on p.15 of Ref. 2)

Conversion factors and significant figures

Some unit equivalence relations, such as those from unit prefixes and their decimal multipliers, are exact. These give rise to exact conversion factors that can be treated in calculations as having an infinite number of significant figures. Another example of an exact equivalence is the cm/in relation given above:

1 in = 2.54 cm   (exactly)

The inch in effect is defined as 2.54 cm exactly.

Inexact conversion factors and constants

Many conversion factors and fundamental physical constants that appear in chemical calculations can be introduced to varying degrees of accuracy (number of digits), and the value we choose depends on the requirements of the calculation. For example, we may have the equivalence relation 1 lb = 453.6 g given by one source (e.g. Ref. 3), and 1 lb = 453.59 g by another source (e.g. Ref. 1). Similarly, the speed of light is given (in Ref. 1, on page facing the back cover) as 2.99792458 × 10⁸ m/s. We may choose to use a rounded value with fewer digits for a particular calculation (though we are always free to use the most accurate value known!) which is fine where data that is not accurately or precisely known is also part of the calculation. The general situation is analogous to computing the area of a circle of a given radius roughly (using π = 3), or more accurately (using π = 3.14159).

Tip: When using inexact conversion factors or constants in calculations, where possible use a sufficient number of significant figures so that the conversion factor or constant does not limit the accuracy of the calculation.

For example, in a calculation of the time it takes light from the sun to reach the earth, using an average distance of 1.5 × 10¹¹ m, it is sufficient to use the value 2.998 × 10⁸ m/s for the speed of light,

(1.5 × 10¹¹ m) / (2.998 × 10⁸ m/s)  =  5.0 × 10² s

where we have rounded and reported the result with the correct number of significant figures. We would have obtained the same result using 2.99792458 × 10⁸ m/s for the speed of light.

See also the Conversions and dimensional analysis topics page.