GENERAL CHEMISTRY TOPICS
Solutions
Solutions: Terminology, definitions. Concentration as a conversion factor. Solution preparation. Dilution calculations. Molarity as a concentration unit based upon mol solute per unit solution volume. Use of molarity. Solution stoichiometry.
Much if not most of the chemistry we are concerned with occurs in solution. Here the basic concepts and terminology necessary for working with solutions is presented. A solution is a homogeneous mixture of two or more substances, typically consisting of a major component called the solvent, and a minor species, designated the solute. Additional solute species are present in more complex solutions. Although a liquid phase solvent is here the most important case, the definition of a solution encompasses solid (e.g. metal alloys) and gaseous mixtures. For the most part this course considers aqueous solutions, that is solutions of compounds in which water is the solvent.
In any quantitative treatment of solutions in chemistry, it is necessary to define the intensive quantity of solution concentration. Concentration of solute at the nanoscale could be expressed as number of solute particles (atoms, molecules, or ions) out of total number of particles (solute + solvent). In the everyday or laboratory macroscale realm, concentration units based upon mass or chemical amounts per unit volume are defined. For example, in laboratory work accompanying this course, the mass-based concentration unit milligrams solute per milliliter of solution (mg/mL) is employed in spectrophotometric measurements of solution concentration. Subsequently, the concentration unit of molarity is introduced (see below) for applications involving solution stoichiometry.
Whatever units of concentration are employed, solution concentration serves as a conversion factor between the two extensive quantities amount of solute and volume of solution. By definition, the product of solution concentration and volume yields the amount of solute. Representing concentration as c and volume as V,
c·V = amount of solute
The units by which solute amount is represented depends on the units used for the definition of solution concentration. For example, for the concentration unit mg/mL, the amount of solute is given in milligrams (mg) when milliliters (mL) is used for solution volume.
Example: If a solution has a volume of 7.00 mL and a concentration of 3.45 mg/mL, how much solute is present in the solution?
Answer: c·V = (3.43 mg/mL)(7.00 mL) = 24.0 mg solute
Since the product of concentration and volume of a given solution yields the amount of solute, it follows that addition of pure solvent to an "initial" solution creates a "final" solution with a lower concentration of solute inversely related to the larger final volume. Any such dilution would be governed by a constant amount of solute in which the product of the concentration and volume of the initial solution (1) is equal to the same product for the final solution (2). These relationships, underlying further work with solutions (see next section) are summarized in the following figure.

Practical aspects of solutions: Preparation and dilution
In preparing solutions, typically a recipe is provided for a solution with a specified composition to be used in a particular application. The appropriate concentration units then depend on the recipe. Prepared solutions are quite useful when they can serve as a "stock" from which other solutions can be conveniently prepared by mixing with additional solvent and/or with stock solutions of other solutes. In other cases, solutions will need to be prepared in more of a customized fashion, and working with solutions may require the interconversion of different concentration units. Examples of "custom" stock solution preparation and concentration interconversions are given below.
Once a stock solution with a known concentration has been prepared, it is often used to prepare other solutions of known but lesser concentration. This latter process is called dilution, and the calculation used in determining how the dilution is to be performed a dilution calculation. If a final volume and concentration is specified for what can be designated as the target solution, the relation
cstock · Vstock = ctarget · Vtarget
holds if we prepare the target solution by adding enough solvent to a volume Vstock to make the final volume of Vtarget. This is because the amount of solute is the same on both sides of the equation.
Example: A stock aqueous solution the sugar glucose has a concentration of 120.00 mg/mL. Describe the preparation of 50.0 mL of 80.0 mg/mL glucose.
Answer: The 80.0 mg/mL solution is the target. The equivalence relation between stock and target becomes (120.00 mg/mL)(Vstock) = (80.0 mg/mL)(50.00 mL). Solving for Vstock yields the volume of stock solution necessary to provide the amount of solute required for the specified target volume and concentration.
Vstock = ctarget · Vtarget / cstock = (80.0 mg/mL)(50.00 mL) / 120.0 mg/mL = 33.3 mL
The preparation would be carried out by measuring 33.3 mL of the stock solution. A 50-mL graduated cylinder would be appropriate to use. Pure water (the solvent) would be added and mixed to make the final solution volume of 50.0 mL.
Note that the equivalence relation used above will always be valid no matter what units are used in defining concentration as long as the same concentration and volume units are used for both sides of the equation.
Molarity as a unit of solution concentration
Molarity is the most important and widely used unit of solution concentration. Molarity, having the symbol M, is defined as moles of solute per liter of solution:
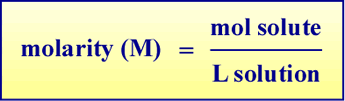
Values of molar concentrations of specific solutes are symbolized using square bracket notation: [NH3], for example, would represent the value of the molar concentration of ammonia in solution. The expression "[NH3] = 3.0 M" corresponds to a solution of ammonia with a concentration of 3.0 mol ammonia per liter of solution.
Using molarity
In working quantitatively with solutions, there are two important practical applications that the use of molarity as a unit of solution concentration well illustrates. These core applications can be presented in the form of the following questions:
(1) How does one prepare a solution of a given solute that has a specified concentration?
(2) Once we have a solution of a given concentration, how can we produce a specified volume of solution of the same solute at a lower concentration?
The answer to the first question provides a custom method to prepare a solution with a target molar concentration based on the formula mass (molar mass) of the solute compound. The mass of solute to be dissolved per unit volume can be calculated, which can then be multiplied by any target volume to obtain total solute mass required. The second answer is an application of the dilution formula using molar concentration for both (stock and target) concentration values.
Example: Suppose we are to prepare 500.0 mL of a 5.00 M sodium chloride solution. The formula mass for NaCl is 58.44. The chemical amount of sodium chloride we will need is given by the product of the given target volume and target concentration:
mol NaCl = mol solute = (0.5000 L)(5.00 M)
= (0.5000 L solution)(5.00 mol solute/L solution) = 2.5 mol
We will treat 2.5 mol as an exact quantity, since it is our target chemical amount for this solution. We will weigh out
(2.5 mol)(58.44 g/mol) = 146.1 g NaCl
To prepare the solution, we completely dissolve and mix 146.1 g NaCl in some volume less than 500 mL, then adjust to the final volume of 500.0 mL by mixing in additional water.
As an example of a dilution calculation, suppose we need to prepare 250.0 mL of 0.150 M NaCl, using the 5.00 M solution described above as a stock solution to be diluted.
Note that letting c1 = [NaCl]initial (that is, the molar concentration of our stock solution, and c2 = [NaCl]final (the target concentration), then V1 and V2 will be the volume of stock solution needed and target volume, respectively, in the general relation
c1· V1 = c2· V2
This relation is always true for volumes and concentrations in a dilution calculation, as long as both concentrations are expressed in the same units, and both volumes are in the same units. For the case of M and L as concentration and volume units, respectively, the equality holds because the product on each side is equal to a constant chemical amount (mol). In this example, we solve for V1, the volume of stock solution (in L) as follows
V1 = c2· V2 / c1 = (0.2500 L)(0.150 M) / (5.00 M) = 0.0375 mol / (5.00 mol/L) = 0.00750 L
So, to perform this dilution, measure 7.50 mL of the 5.00 M NaCl stock solution, and dilute with additional water to a final volume of 250.0 mL.
Molarity as a conversion factor and solution stoichiometry
Solution concentrations expressed in M sets up an equivalence relation
N mol solute = 1 L solution
where N is numerically equal to the molar concentration of the solute. So, multiplication of soluton concentration of a solute by solution volume in L yields total chemical amount (mol) solute:

Note that for dissolution of ionic compounds such as (NH4)2SO4 and Pb(NO3)2, the concentrations of ionic species in solution will depend explicitly on the stoichiometry of the formula of the compound, which determines the stoichiometry of the dissolution equation.
Example: For a 4.00 M solution of ammonium sulfate, what is the concentration of ammonium ions in the solution?
To help conceptualize the case at hand, write out the chemical equation for the dissolution process. The equation represents the formation of the solution from the mixing of solute, initially solid ammonium sulfate, mixed homogeneously in solvent water. (See the ionic and net ionic equations page for background.)
As ammonium sulfate is a soluble ionic compound, it is a strong electrolyte. The dissolution equation shows this, as the products are aqueous ions that are homogeneously distributed and move freely throughout the solution. The aspect to focus on here is that the dissolution of one formula unit creates two ammonium ions and one sulfate ion. Note that the subscript of 2 outside the parentheses in the formula for the compound ammonium sulfate becomes the leading stoichiometric coefficient for the ammonium ion in aqueous solution.
With this stoichiometry in hand, it becomes clear that the formal concentration of ammonium sulfate must be multiplied by this factor of 2 to obtain the resulting concentration of ammonium ion in solution. Thus for a 4.00 M ammonium sulfate solution, the concentration of ammonium ions is 8.00 M. Similarly, the concentration of sulfate is 4.00 M, since each formula unit of ammonium sulfate contains one sulfate ion.
Defining the concentration unit of molarity and the resulting equivalence between chemical amount (mol) and volume allows the expression of stoichiometric relationships in a chemical reaction taking place in solution by reactant solution volumes. To illustrate this somewhat generally, suppose there are two solutions denoted solution A and solution B. These solutions contain solute species A and B respectively, that when mixed undergo a reaction
a A + b B → products
with the reactants in balance according to their stoichiometric coefficients a and b. Then given the solute concentrations of [A] and [B] respectively, a specified volume of solution A can be converted by calculation to the volume of solution B that would react completely with A when the two solutions are mixed. Another way to state this is that the two volumes are stoichiometrically equivalent. Note that it is assumed in this reaction-in-solution scenario that whatever A and B are present are 100% converted to products. This is known as theoretical yield of products.
The process for this calculation is to multiply the volume of solution A by its concentration - this yields mol A - then by the stoichiometric ratio of B to A in the balanced chemical equation for the reaction (for the chemical equation above, this factor would be b/a), yielding mol B, then finally dividing by the molar concentration of solution B. This is represented in the schematic diagram below.
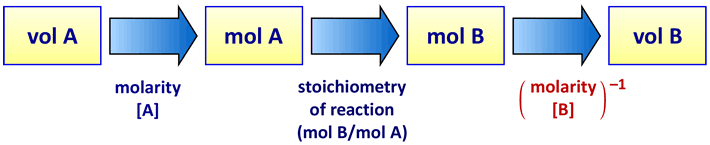
Each step (represented by the blue rightward arrows) of the three-step process converting the four quantities shown in boxes is associated with a conversion factor. The first conversion factor, for volume A to mol A, is the molar concentration of solution A, [A]. The second conversion, mol A to mol B, is the stoichiometric ratio of reaction (i.e. the ratio of the reaction stoichiometric coefficient for B to that of A). The third conversion factor is the inverse of the molar concentration of solution B, [B]−1, converts mol B to volume B.
Stoichiometric equivalence in precipitation reactions
Considering a specific example of a precipitation reaction and stoichiometric equivalence, suppose 50.0 mL of a 4.00 M ammonium sulfate solution is to react completely with a 2.50 M barium chloride solution according to a precipitation reaction
(NH4)2SO4(aq) + BaCl2(aq) → 2 NH4Cl(aq) + BaSO4(s).
What volume of the barium chloride solution is just sufficient to react with all of the ammonium sulfate? In other words, the volume of barium chloride solution that is stoichiometrically equivalent to 50.0 mL of 4.00 M ammonium sulfate solution must be determined. Again, stoichiometric equivalence means that neither reactant is in excess or limiting. The amounts of each are exactly balanced according to the stoichiometry of the reaction. How the schematic above is applied to this case is illustrated in the next figure:
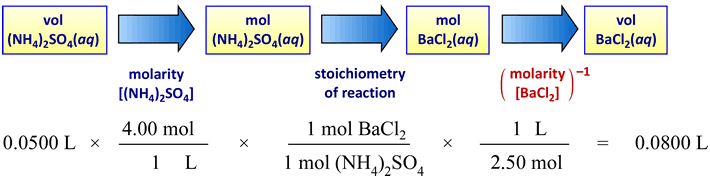
Since here the reactants have a one-to-one stoichiometry, the chemical amounts (in mol) of each can be directly compared. If the reactants are in stoichiometric equivalence, then
(4.00 M)(50.0 mL) = (2.50 M)(VBaCl2)
VBaCl2 = (4.00 M)(50.0 mL) / 2.50 M = 80.0 mL.
Example 2: The precipitation reaction between solutions of sodium phosphate and barium chloride is studied in the CHEM 101L Limiting Reactant lab. The balanced "molecular" or formula unit chemical equation for the reaction is
2 Na3PO4(aq) + 3 BaCl2(aq) → 6 NaCl(aq) + Ba3(PO4)2(s).
Suppose 40.0 mL of a 0.0262 M sodium phosphate solution is to react completely with a 0.0414 M barium chloride solution. Calculate the stoichiometrically equivalent volume of the barium chloride solution.
In this case the stoichiometry of reaction is 3 : 2 for the reactants forming the precipitate product. The schematic for conversion of volume sodium phosphate solution into the stoichiometrically equivalent volume of barium chloride solution is shown in the figure below.
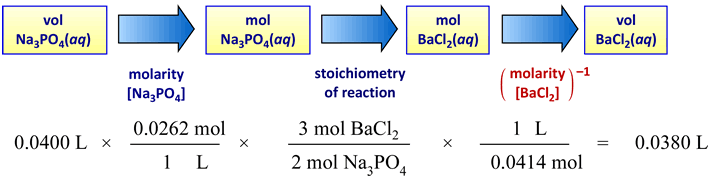
The same calculation shown in alternate format:
VBaCl2 = (40.0 mL) × { 0.0262 M / 2 } × { 3 / 0.414 M } = 38.0 mL.
In cases for which the proportions of two reactant solutions are not in stoichiometric equivalence, one or the other reactant will be in stoichiometric excess, while the other will be what is referred to as the limiting reactant. Revisiting the example above, what would happen if a volume of barium chloride solution (of the stated concentration) greater than 38.0 mL was mixed with the specified volume and concentration of the sodium phosphate solution? It helps in this analysis if the net ionic equation for this reaction is employed, which in this case is
3 Ba2+(aq) + 2 PO4−3(aq) → Ba3(PO4)2(s).
This equation shows that the reaction is actually the formation of the insoluble product by the combination of barium ions and phosphate ions provided by the separate solutions. If more than 38.0 mL of the barium chloride solution is provided, this will include barium ion in excess of that necessary for 100% conversion of the phosphate ion present into the product Ba3(PO4)2(s) as precipitate. Conversely, the amount of phosphate ion present would be insufficient to convert all of the barium to product. The theoretical yield, or maximum possible yield of product will be that calculated for 100% conversion of the limiting reactant.