BIOCHEMISTRY TOPICS
Bioenergetics I.
Thermodynamic principles. Chemical thermodynamics Biochemical standard state. Adenosine triphosphate and other high-energy phosphoryl compounds Substrate-level phosphorylation
Thermodynamics: Summary of principles
- The first law of thermodynamics: Energy is conserved
- The second law of thermodynamics states that total entropy increases for spontaneous processes
- The free energy change (ΔG) determines the spontaneity of a process
- Standard free energy change (ΔG°) can be calculated from equilibrium concentrations, and ΔG can be calculated from ΔG° and actual (generally nonequilibrium) concentrations
- Life obeys the laws of thermodynamics, and living organisms are open systems that maintain nonequilibrium states and tend to operate at a steady state
Quantitative relations of chemical thermodynamics. The third and fourth principles can be expressed in equation form. These relations are the most important equations for applying thermodynamics to chemical or biochemical reactions, and you should be thoroughly familiar with them.
For any biochemical reaction, or many processes such as conformational or phase equilibria, the free energy change, ΔG′ for that reaction or process is given by
ΔG′ = ΔG°′ + RT·ln Q′
where ΔG°′ is the biochemical standard free energy change (see below; in all these relations, the prime [′] denotes biochemical standard conventions), and Q′ is the reaction quotient expression for the biochemical reaction as represented in a biochemical (chemical) equation, the value of which depends on the activities of the product and reactant species in the equation. Routinely, activities are taken as approximately equivalent to concentrations, although this approximation becomes increasingly inaccurate as concentrations or ionic strength increase. When ΔG′ is negative, the reaction under those conditions is said to be exergonic, and the forward reaction (reactants → products) will be the spontaneous direction. In other words, in order to approach equilibrium, reactants must undergo net conversion to products. When ΔG′ is positive, the reaction under those conditions is said to be endergonic, and the reverse reaction (products → reactants) will be the spontaneous (exergonic) direction. In other words, in order to approach equilibrium, there must be a net conversion of products to reactants. When ΔG′ = 0, the reaction is already at equilibrium, conditions in which there is no net conversion of reactants to products or vice-versa. From the viewpoint of kinetics, the rates of the two opposing processes (reactants → products and products → reactants) are equal, which is a reminder that chemical equilibrium is a dynamic, not static, condition.
The above relation is the fundamental equation of chemical thermodynamics, and from it another extremely useful equation can be readily obtained. Since ΔG′ = 0 at equilibrium, the left hand side of the above equation is set to zero. At the same time, the concentrations of reactants and products are equilibrium concentrations, so Q′ = K′eq. Making this substitution and rearranging gives
ΔG°′ = − RT·ln K′eq
which is the quantitative expression of the statement that standard free energy change (ΔG°) can be calculated from equilibrium concentrations.
Standard free energy and biochemical standard
In the term ΔG°, its " ° " symbol indicates that we are dealing with a standard free energy change for the reaction. The value of ΔG° depends on the definition of a thermodynamic standard state. Since we need only concern ourselves with changes in free energy, we can define any reference state we please, and we may as well choose it to be the most reasonable or convenient for our purposes. In physical chemistry, the standard state is defined as follows:
(1) Temperature T is specified
(2) Pressure P is 1 bar [ 1 bar = 105 Pa = (1/1.01325) or 0.986923 atm ]
(3) Activity of solutes in solution is 1 M (activity is roughly equivalent to concentration for dilute solutions)
Setting the activity to 1 simplifies the calculation of ΔG. The temperature can be any value, but must be specified. Usually 298.15 K (25.00°C) is chosen. The physical chemistry standard state is implicit in the designation ΔG°, which corresponds to the free energy change for the complete conversion of the pure reactants in their standard states into the pure products in their standard states. In view of what we said above about choosing a convenient standard state, it makes sense to define a standard state more specifically tailored to biochemical applications. For instance, it is nonsensical to set the standard state for the activity of H+ to be 1 M (i.e. pH = 0), when most physiological processes take place in a buffered system held near pH = 7. The free energy change for biochemical standard state - symbolized as ΔG°′ - depends on a standard state, or a set of standard conditions, defined as follows:
(1) Activity of pure water is assigned a value of 1
(2) pH is assumed to be 7
(3) Hydrogen ion activity also assigned a value of 1
(4) Standard state of an ionizable substance is defined in terms of the total concentration of all of its forms
Water is the "standard" solvent, or medium, for biological systems. Setting its activity to 1 allows us to neglect the [H2O] term in Q′. Since physiological pH is near neutrality, a standard state of pH 7 is reasonable. A hydrogen ion activity of would correspond to pH 0. As for water, setting the activity of H+ to 1 allows us to neglect the [H+] term in Q′when pH is assumed to be 7. There are many ionizable functional groups in biochemical systems. Many of these exist at pH 7 in significant amounts of more than one form. For example, phosphate in its H2PO4− form has a pKa of 7.2 at 25°C. This means that although in the biochemical standard state phosphate exits mostly as H2PO4− and HPO42−, we are able to treat it as one term in Q, ["phosphate"] or {Pi], meaning the sum of [H2PO4−] and [HPO42−] and insignificant amounts of other forms may exist at pH 7.
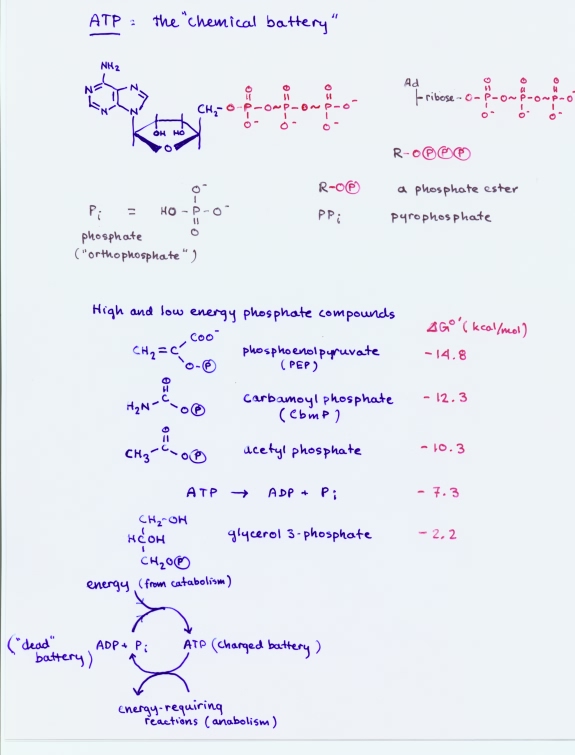
Adenosine triphosphate (ATP)
ATP is the nucleotide consisting of the base adenine (red numbers in figure), the sugar ribose (green numbers), and a triphosphate group group in an ester linkage with the 5'-hydroxyl of the ribose.

ATP is a major product of metabolism, specifically the energy-yielding processes of catabolism. In turn, ATP serves as a ubiquitous carrier of metabolic energy in the form of high phosphoryl transfer potential. This is usually associated in ATP with the phosphoric anhydride bonds within the triphosphate group. As a nucleotide, ATP is a building block for nucleic acid synthesis, while as an energy carrier, it provides chemical energy to drive anabolic processes.
Substrate-level phosphorylation
Substrate-level phosphorylation is a specific type of metabolic reaction involving phosphate-containing substrates and products, and it entails a direct chemical coupling of an energy-liberating biochemical reaction with the energy-conserving formation of a "high energy" product, typically ATP. An example of substrate-level phosphorylation occurs in glycolysis when phosphoenolpyruvate (PEP) reacts with ADP to form ATP and pyruvate, a reaction catalyzed by the enzyme pyruvate kinase.
Phosphoryl transfer potential, like any form of potential energy, can be measured relative to a reference. Here, the hydrolysis reaction with water - that is, phosphoryl group transfer to water - serves as a reference. The hydrolysis reaction is effectively always a thermodynamically favorable process, with biochemical free energy change negative in sign (ΔG°′ < 0). The greater the phosphoryl transfer potential of a given compound bearing a phosphoryl group, the more energetically favorable is its hydrolysis reaction. In the case of PEP, hydrolysis would release a considerable amount of energy. In the metabolic context of glycolysis, instead of undergoing hydrolysis, PEP transfers its phosphoryl group to ADP, thereby conserving much of the energy of PEP hydrolysis in the form of a phosphoric anhydride bond in ATP.
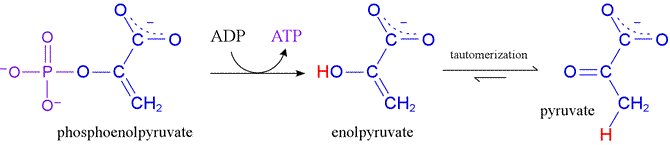
The question that naturally arises from this example concerns the chemical basis for the very high phosphoryl transfer potential of PEP, and more generally the chemical considerations that are important in determining the relative phosphoryl transfer potential of phosphorylated compounds. For PEP, the transfer of its phosphoryl group to ADP would, as represented in the figure above, lead directly to an enol form of the product pyruvate. Hydrolysis of PEP to yield enolpyruvate would be favorable as a first step, while the subsequent tautomerization step provides additional thermodynamic favorability. In comparison, the free energy of hydrolysis of ATP, while considerable, does not match that of PEP.
The more general question is best answered on a case-by-case basis, but another prominent factor in compounds with high phosphoryl transfer potential is resonance stabilization of the products. This is most clearly seen in the case of acyl phosphates, which gain the resonance stabilization of the carboxylate group upon phosphoryl transfer. A metabolic example of substrate-level phosphorylation involving an acyl phosphate is provided by the phosphoglycerate kinase reaction.
Related topics pages: