BIOCHEMISTRY TOPICS
Problems in acid-base chemistry: Buffers
Understanding buffers. Buffer pH calculation from composition. Change in pH of buffer upon addition of strong acid. Composition of a buffer calculated from a target pH. Preparation of a buffer, calculations for a target pH and total volume. Physilogical buffering.
Problem 9-11. (ECA4, p.210) Modified
(a) Write the chemical equation for the acid dissociation of imidazole hydrochloride and the corresponding expression for Ka. Do the same for base hydrolysis reaction and Kb for imidazole.
(b) Calculate the pH of a 1.00-mL solution containing 1.00 g of imidazole (FM 68.08) and 1.00 g of imidazole hydrochloride (FM 104.54).
(c) Calculate the pH of the solution if 2.30 mL of 1.07 M HClO3 are added to the solution.
(d) How many milliliters of 1.07 M HClO3 should be added to 1.00 g of imidazole to give a pH of 6.993?
Solution:
(a) The acid dissociation equation is a representation of a general Brønsted-Lowry acid as reactant, with products the conjugate base and H+. A positively-charged acidic species can be represented as BH+, and thus its acid dissociation equation as
BH+ → H+ + B
The base hydrolysis of the neutral base B would be written as
B + H2O → BH+ + OH−
More specifically, the equations for imidazole hydrochloride and imidazole are shown below, along with the corresponding expressions for the equilibrium constants Ka and Kb.
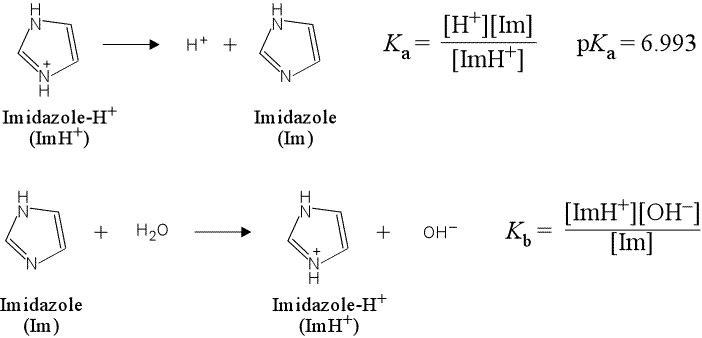
Here we have used Im and ImH+ as convenient, yet more specific abbreviations for the neutral base imidazole and its conjugate acid. Note that ImH+ is not a compound we could procure "off the shelf", but would be found as a salt with an anion, such as Cl−, as in imidazole hydrochloride.
(b) In this part we can apply the Henderson-Hasselbalch equation. Since the volumes effectively cancel in the concentration ratio within the log term, we can choose to work with moles and take the log of the mole ratio. Bearing in mind that 1.00 g of both the imidazole and the imidazole hydrochloride are included, we can write
pH = 6.993 + log{ mol Im / mol ImH+ }
pH = 6.993 + log{ (68.08)–1 / (104.54)–1 }
pH = 6.993 + 0.186 = 7.179
which gives us pH = 7.18, when reported to the nearest 0.01 unit.
(c) Starting with the solution above, we add a defined amount of strong acid, which will react completely with the base form of the buffer. The strong acid here is chloric acid, HClO3, but any strong acid would react similarly. The concentration of the strong acid is 1.07 M, so 2.30 mL will contain
(1.07 mmol/mL)(2.30 mL) = 2.46 mmol H+
(Note that since chloric acid dissociates completely in water we can equate its concentration with that of H+.) The 2.46 mmol H+ will convert exactly the same amount of Im into ImH+. We can set up a table to show this, but to fill in the table, we need to explicitly calculate the amounts of Im and ImH+:
mmol Im = (1.00 x 103 mg) / ( 68.08 mg/mmol ) = 14.69 mmol
mmol ImH+ = (1.00 x 103 mg) / ( 104.54 mg/mmol ) = 9.566 mmol
Now set up the table:
| ImH+ | = | H+ | + | Im | ||||
| initial concentration | 9.566 mmol | 2.46 mmol | 14.69 mmol | |||||
| final concentration | 9.566 + 2.46 mmol | - | 14.69 – 2.46 mmol | |||||
This table is similar to the tables we construct in solving equilibrium calculations (as in the weak acid and weak base problems), but this is not really an equilibrium problem since the reaction goes to completion (equilibrium greatly favors products). In that sense, the treatment of this case is akin to that of the pH of a strong acid, in which we assume complete dissociation of the acid. Therefore, we do not have to solve for x (x = 2.46 mmol in this case). Doing the sum and difference in the bottom row of our table we have:
mmol Im = 12.23 mmol
mmol ImH+ = 12.026 mmol
We simply plug these values into the Henderson-Hasselbalch equation to calculate the new pH:
pH = 6.993 + log{ mol Im / mol ImH+ }
pH = 6.993 + log{ 12.23 / 12.026 }
pH = 6.993 + 0.0073 = 7.0003
which gives us pH = 7.00, when reported to the nearest 0.01 unit.
(d) If we start with just the base imidazole, and add strong acid to it, then the amount of base converted to the conjugate acid will correspond directly to the amount of strong acid added. We already know that 1.00 g of imidazole is 12.23 mmol, and we are given a target pH of 6.993, which happens to be the pKa of ImH+. This simplifies the problem, since we know from the Henderson-Hasselbalch equation that pH = pKa when the ratio of base and acid is exactly 1. Thus we can see immediately that exactly half of the imidazole must be protonated by addition of the strong acid, converting it into its conjugate acid form, ImH+. The problem can be solved in one calculation as shown below:
mL HClO3 to add = {(1.00 x 103 mg) ( 68.08 mg/mmol )–1} / {2 (1.07 mmol/mL)} = 6.86 mL.
If we had a different target pH for this problem, then we could create a table, similar to the one above, and solve for the moles of H+ from the strong acid needed to give the mole ratio of the basic and acidic forms of the buffer that produces the target pH. As an equivalent approach (which we also make somewhat more general), we could solve an equation derived by rearrangement of the Henderson-Hasselbalch equation:
pH – pKa = log{ (mol B – x) / x }
10pH – pKa = (mol B – x) / x
x = (mol B) / ( 1 + 10pH – pKa )
Whatever units are used for B will determine the units for x. So if mmol B is used, then x will be given in mmol. So for example, if we let B be imidazole, so that pKa is 6.993, and use 1.00 g Im = 14.69 mmol, and set a target pH of 7.40, then the above formula gives us x = 4.135 mmol. This is provided by (4.135 mmol) / (1.07 mmol/mL) = 3.86 mL of 1.07 M HClO3.
Homework problem for Lecture 10
How many milliliters of 2.50 M NaOH should be added to 1.00 g of the acid form of HEPES to produce a solution of pH 8.00?
Instructor's note: Inspired by Harris, ECA3, Problem 9-11(d) (p.190) Solution author: Jeff D Cronk. Created 02-08-06.
Solution: The relevant chemical reaction here (shown below) is that of HEPES acid with hydroxide, producing HEPES base and water. This is the reverse of the base hydrolysis reaction for HEPES base, and has a very favorable equilibrium constant:
Keq = 1/Kb = Ka/Kw.
We find (in Table 9-2, p.184 of Harris) that the pKa of HEPES acid is 7.56, and its formula mass is 238.30.

Calculating Ka, and then substituting it into the expression for Keq,
Ka = 10− pKa = 2.8 × 10−8.
Keq = 1/Kb = Ka/Kw = (1.0 × 10−14 / 2.8 × 10–8) = 2.8 × 106
This was not part of the problem, but is provided as background. The point of this excursion is to emphasize that the operative chemical principle here is that weak acid reacts completely with strong base.
| HEPES-H | + | OH– | = | HEPES– | + | H2O | |||
| initial amount | N | x | 0 | (constant) | |||||
| final amount | N – x | 0* | x | ||||||
This table is similar to the tables we constructed in solving equilibrium calculations (as in the weak acid and weak base problems), but this is not really an equilibrium problem since the reaction goes to completion (equilibrium greatly favors products).
N = initial amt HEPES acid = 1.00 g / 238.30 g mol–1 = (238.30)–1 mol. = 4.1964 mmol (3 significant figures)
If we start with just the acid form of HEPES (represented as HEPES-H in the table), and add strong base to it, then the amount of HEPES acid converted to its conjugate base form will correspond directly to the amount of strong base added. We already know that 1.00 g of HEPES acid is 4.1964 mmol, and we are given a target pH of 8.00, while the pKa of HEPES acid is 7.56. We solve a general equation derived by rearrangement of the Henderson-Hasselbalch equation:
pH – pKa = log{ (mol HEPES base, final ) / ( mol HEPES acid, final) } = log{ x / ( N – x) }
10pH – pKa = x / ( N – x)
x = N(10pH – pKa) / ( 1 + 10pH – pKa )
Whatever units are used for N will determine the units for x. So if mmol HEPES acid is used, then x will be given in mmol. Substituting the values for pH – pKa = 8.00 – 7.56 = 0.44 and N = 4.1964 mmol, and solving the equation gives us x = 3.0786 mmol. Thus we need to add 3.0786 mmol to the 1.00 g of HEPES acid to get a calculated pH of 8.00. This is provided by (3.0786 mmol) / (2.50 mmol/mL) = 1.23 mL of 2.50 M NaOH.
Homework assignment 3 (240PHW-03, due Wednesday 11 Feb)
(1) Describe three different ways to prepare 100.0 mL of 50.0 mM CHES buffer at a target pH of 8.80. Perform the necessary calculations using CHES acid (HA, pKa = 9.39, FM 207.29), sodium salt of CHES conjugate base (FM 229.27), 2.50 M HCl and 0.125 M NaOH. Show all calculations as clearly as you can. Report the masses of CHES acid and/or the conjugate base to the nearest 0.001 g and volumes of HCl or NaOH to the nearest 0.01 mL.
(2) Dividing the buffer prepared according to the above specifications into two 50.0 mL portions, calculate the pH resulting from (a) adding 10.00 mL of 50.00 mM HCl to one portion, and (b) adding 10.00 mL of 50.00 mM NaOH to the other portion.
Solution: The buffer system consists of the conjugate pair HA (CHES acid) / A− (CHES conjugate base, an anionic species. We'll calculate the chemical amounts, in mmol, for each member of the conjugate pair of buffer species according to the solution to the "two equations in two unknowns" problem. We let N represent the total mmol of buffer species, a the amount of HA in mmol, and b the mmol amount of A−.
N = a + b
r = b / a = 10pH – pKa
Let's obtain the values for N and r for this case.
N (mmol) = (Target conc., mmol/L)(Target vol., L) = (Target conc., mmol/mL)(Target vol., mL)
N (mmol) = (50.0 mmol/L)(0.1000 L) = 5.00 mmol
For the ratio r of conjugate weak base to weak acid,
r = b / a = 10pH – pKa = 10(8.80 − 9.39) = 10−0.59 = 0.25704
If we solve the equation r = b/a for b, then substitute that result into the equation N = a + b , we obtain a general solution for all such buffer preparation calculations in the form
N = a + b = a + ra = a(1 + r)
a = N / (1 + r)
b = N − a
where the value of a obtained by putting values for r and N into the second equation is in turn (along with N) plugged into the third equation, thus finding b:
a = N / (1 + r) = 5 / 1.25704 = 3.978
b = N − a = 5 − 3.978 = 1.022
Calculating the mass in grams of each buffer species represented by these chemical amounts,
CHES acid: (3.978 mmol)(207.29 mg/mmol) = 825 mg = 0.825 g
sodium CHES: (1.022 mmol)(229.27 mg/mmol) = 234 mg = 0.234 g
For the other two methods, we use the values a and b obtained in the following manner:
Method 2: Using just the weak base form of the buffer (sodium CHES) and strong acid (here we are given 2.50 M HCl(aq)), which provides H+(aq). Since the full chemical amount N must be initially supplied by the base form, and the quantity a is the chemical amount of H+ that must be supplied by strong acid to convert the base form of the buffer to its conjugate acid so that b/a = r, we have
N mmol sodium CHES would in this case be provided by (5. mmol)(229.27 mg/mmol) = 1146 mg
a mmol H+(aq) from HCl(aq) to convert a mmol A− to HA: (3.978 mmol) / (2.50 mmol/mL) = 1.59 mL
Note that this results in the final amounts of HA and A− that sum to 5 mmol and are in the correct ratio to yield the target pH:
Final mmol HA = a mmol = 3.978 mmol
Final mmol A− = (N − a) mmol = b mmol = (5 − 3.978) mmol = 1.022 mmol
Method 3: Using just CHES acid and 0.125 M NaOH.
Since the full chemical amount N must be initially supplied by the acid form; the quantity b represents the chemical amount of OH− that must be supplied by strong base to convert the acid form of the buffer to its conjugate acid so that b/a = r
N mmol CHES acid would in this case be provided by (5. mmol)(207.29 mg/mmol) = 1.0365 g
b mmol OH−(aq) from NaOH(aq) to convert b mmol HA to A−: (1.022 mmol) / (0.125 mmol/mL) = 8.18 mL.
To conclude part (a) of this problem, we summarize the three preparations:
Method 1: Measure 0.825 g CHES acid, transfer to water, dissolve and mix, then weigh 0.234 g of sodium CHES, transfer quantitatively to solution, dissolving and mixing completely, and then making up the final volume to 100.0 mL with water.
Method 2: Weigh 1.146 g sodium CHES, transfer and dissolve completely in < 100 mL water, then measure 1.59 mL 2.50 M HCl, transfer completely and mix with enough more water to make the final volume 100.0 mL.
Method 3: Measure 1.0365 g CHES acid, transfer to water, dissolve and mix, then add 8.18 mL 0.125 M NaOH, mix, and then add enough water to make the final volume 100.0 mL.
(b) To solve this problem, we'll use the Henderson-Hasselbalch equation in the form
pH = pKa + log{ mmol weak base / mmol weak acid }
Since the 100.0 mL will be divided into two 50.0-mL portions, the chemical amounts in each portion are exactly half of what was present in the full 100 mL. Thus, in each 50.0-mL portion, N = 2.5 mmol (again, we'll assume exactly 2.5 and just use reasonable numbers of digits in calculations and reporting results), and a = 3.978/2 = 1.989 mmol, b = 1.022/2 = 0.511 mmol. The pH is of course is still 8.80. When 10.00 mL of 50.00 mM HCl is added, this delivers (0.05000 mmol / mL)(10.00 mL) = 0.500 mmol H+ to the buffer portion, which will react with (subtracting) 0.500 mmol A− and produce (adding) 0.500 mmol HA. So we can calculate the new pH as:
pHnew = 9.39 + log{ ( 0.511 − 0.500 ) / ( 1.989 + 0.500 ) } = 9.39 + log (0.011 / 2.489)
pHnew = 9.39 + log 0.004419 = 9.39 − 2.35 = 7.04
Using the same values for a and b (scaled to 50.00 mL of buffer) as above, the corresponding calculation for addition of strong base:
(0.05000 mmol / mL)(10.00 mL) = 0.500 mmol OH− added.
pHnew = 9.39 + log{ ( 0.511 + 0.500 ) / ( 1.989 − 0.500 ) } = 9.39 + log (1.011 / 1.489)
pHnew = 9.39 + log 0.6790 = 9.39 − 0.17 = 9.22
Example problem 4. Physiological buffering by CO2(aq)//bicarbonate. Defining "total dissolved CO2" or "total carbonate pool" as including CO2(aq) all species derived from it (H2CO3(aq), HCO3−(aq), CO32−(aq)) it is found that a sample of blood plasma has a total dissolved CO2 concentration of 2.62 × 10−2 M. (i) Calculate the ratio [HCO]/[CO2] in blood plasma at pH 7.4. (ii) Calculate the change in pH when 10 mmol H+ per L is added under conditions where cannot be released. (iii) Repeat the calculation for an open system in which excess CO2 can be released.