Lecture 2. Life, thermodynamics, and water
Friday 2 September 2016
Life and thermodynamics. The geometric, electronic, and bulk properties of water relevant to biological systems. Noncovalent (weak electrostatic) forces. The hydrophobic effect: Nonpolar and amphipathic species in water. Thermodynamic analysis of the hydrophobic effect. Colligative properties; osmosis, diffusion, and dialysis.
Reading: Voet, Voet and Pratt, 4th ed. (VVP4e); Chapters 1 and 2.
Summary
Biological systems are subject to the same physicochemical laws that govern non-living systems. It is important therefore to understand explicitly how basic thermodynamic principles are applied in biochemistry and biology. Therefore we undertake a review of the thermodynamics appropriate for application to biological systems. For example, we can usually treat processes in living organisms and tissues as occurring at constant pressure and temperature, with little or no change in volume. Thermodynamic methods valid in general for such processes will be useful in this specific biological context. To illustrate, the free energy function is used to interpret both the formation of a DNA double helix from separate single strands and the hydrophobic effect. The physical and chemical properties of water are of great relevance to biochemistry. The hydrophobic effect, an especially important case, is a consequence of the properties of water and aqueous environments.
A brief review of chemical thermodynamics
The first law of thermodynamics is equivalent to the law of conservation of energy. For example, in a process occurring at constant pressure and volume involving exchange of heat between a system and its surroundings, the enthalpy change (ΔH) for the system will be exactly balanced by ΔH for the surroundings so that the net ΔH is zero. Conservation of energy applies to all processes, but says nothing about the direction that a process obeying it will operate in. A further aim of thermodynamics is to be able to predict whether or not a process will occur within a system without the input of energy from the surroundings. If so, the process is said to be spontaneous. In order to make such predictions, it is first necessary to define entropy, S. Roughly speaking, entropy is a measure of the number of ways that energy can be distributed within a system. The second law of thermodynamics states that the total entropy of the system and surroundings always increases for a spontaneous process.
For biochemical systems, it would be convenient to have a means to evaluate whether or not a process is spontaneous without having to consider the surroundings. The state function known as Gibbs free energy, G (sometimes referred to simply as free energy), which is defined by the equation G = H − TS that combines the state functions enthalpy and entropy (T is the temperature in K), is the key quantity that allows us to make this determination. The change in free energy of a system for a process occurring at constant temperature is given as ΔG = ΔH − TΔS. A spontaneous process corresponds to a decrease in the free energy of the system.
Key thermodynamic equations for biochemistry
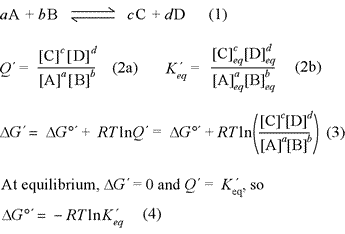
The relationship between free energy and chemical equilibrium is one of the most important results of chemical thermodynamics, and it retains this status in biochemistry. The equations at right, (1) - (4), are the key thermodynamic relations that are essential for you to know. The equations are general in form, so it is also necessary to understand how they are used in specific examples. The quantity ΔG°′ is the biochemical standard free energy change, which is based on the definition of a biochemical standard state. In all these relations, the prime [′] denotes biochemical standard conventions in order to clearly distinguish from chemical convention (physical chemistry standard conventions) for which all the relations above are the same, sans prime symbol. The key distinction to bear in mind for these conventions is for the standard hydrogen or hydronium ion concentration. While the physical chemistry standard [H+] is 1 M (just like for any solute species), in the biochemical convention the standard [H+] is specifically defined as 1 × 10−7 M, or pH 7.
Properties of water
Since so many of the processes of living organisms occur in aqueous media, it is of fundamental importance to understand physicochemical properties of water. Given the complexity of the liquid state, especially that of water, accomplishing this is much more of a challenge than one might first imagine. Let us nonetheless at least consider some of the outstanding features of water, and try to get at what are the most relevant and important from a biochemical viewpoint. With water making up most of the weight of typical organisms, it is appropriate to think of water as the solvent of life, and we'll examine the properties of water as a solvent and the principles of aqueous solution chemistry.
One very notable feature of water is its great capacity and tendency to form hydrogen bonds with itself and solutes with hydrogen-bonding ("H-bonding") groups. This underlies water's great cohesiveness, manifest in some unusual properties such as high melting point, boiling point, and surface tension. Molecules with a number of functional groups capable of hydrogen bonding with water tend to be quite soluble in water. Since water is a polar molecule, it also interacts well with ions and polar molecules.
Water is unquestionably an excellent solvent for many polar and charged species, yet it is a rather poor solvent for nonpolar molecules. Amphipathic molecules such as detergents or phospholipids can form micelles or bilayer structures in which the nonpolar portions of the amphipathic molecules are are sequestered together, while the polar or charged portions are exposed to the aqueous surroundings.
What is the basis of the solvent properties of water? The interactions of water with ions, dipoles, and H-bond acceptors and donors are strong. The dipole of water interacts strongly with charges, and we should note here that the rather large dielectric constant of water weakens electrostatic forces between charged solute groups. Water molecules ought to be able to interact somewhat favorably with nonpolar species by van der Waals attractions.
If we are to understand water as a solvent, we will have to venture beyond "like dissolves like" with some more careful analysis. If we imagine a process in which initially separated water and solute mix, the thermodynamics are tricky because although water interacts so well with solutes, its interacts with quite well with itself, as may some solutes such as salts. Thus, for the case of an ionic solid that dissolves endothermically, ΔH of the process is not favorable, but ΔS of forming the more dispersed solution is positive (and thus favorable). For solutes with nonpolar character, on the other hand, the interactions between solute molecules in the undissolved initial state and between solute molecules and water molecules in the dissolved state are both considerably weaker. Yet it is still possible for the solute-solvent interactions to be a little better than the interactions in the separated materials. The enthalpy change (ΔH) of the process is then slightly negative; even so, the solubility may still be quite low, indicating that ΔG is positive. We would be led in this case to the counterintuitive conclusion that ΔS is negative. This large negative ΔS for the formation of aqueous solutions of nonpolar solutes is the basis of the what is usually called the hydrophobic effect.
Chemical properties of water: Acid-base chemistry
Please review these topics: Autoionization of water and pH. Acids, bases, and buffers in aqueous systems.
In biochemistry, especially in discussion of amino acid and protein chemistry, we will make frequent use of the concept of pKa of an ionizable group. Starting with the chemical equation for the ionization of a weak acid (see figure below, left), the acid dissociation equation (top equation), we derive the usual equilibrium expression, giving the equilibrium constant the special designation Ka (2nd equation). Taking the negative logarithm (base 10) of both sides of this equation leads to a definition of pKa in terms of pH and the log(10) of the ratio of concentrations of the anionic conjugate base and unionized acid (not shown).
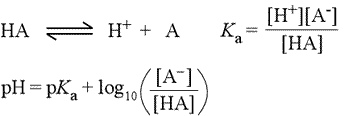
This equation can be rearranged to express pH in terms of pKa and the log ratio of conjugate base to acid, yielding what is known as the Henderson-Hasselbalch equation (3rd equation, at left).
These equations are very useful for buffer calculations and in determining the proportions of conjugate pairs that exist at a given pH. It is easy to see, for instance, that at a pH equal to the pKa of a weak acid HA, the population of unionized acid molecules is exactly balanced by the number of molecules of the conjugate base. At a pH above that of the pKa, the anionic form will predominate, and at low pH, the unionized acid species is favored.
Exercise: Derive the Henderson-Hasselbalch equation for the ionization equilibrium BH+ = H+ + B:. Which form predominates at low pH? Compare this equilibrium with that for the dissociation of the neutral acid HA above, and consider the effect of transferring the ionizable group from an aqueous environment to a non-polar environment. Are the respective pKa's affected equally, or is one affected more than the other? Explain.