Lecture 32. Bioenergetic principles
Wednesday 30 November 2016
The PDH and citric acid cycle reactions generate electron donors at a relatively low reduction potential. Transfer of electrons from metabolically-generated electron donors (NADH, FADH2) via the electron transport chain to oxygen, which is at a high reduction potential. Exergonic electron transfers drive the formation of a transmembrane electrochemical gradient. The free energy of the electrochemical gradient (a transmembrane ΔpH) drives the synthesis of ATP.
Reading: VVP4e - Ch.18, pp.581-607.
Summary
One problem that we can imagine faced the earliest cells is that a membrane-enclosed concentration of macromolecules creates a transmembrane chemical potential difference that cannot be equalized by diffusion of the macromolecules themselves. Instead, water diffuses into the cell since this lowers the chemical potential difference. Our imaginary protocell would have to cope with the possibility of osmotic crisis due to this influx of water. This could be accomplished if the cell could somehow set up an opposing concentration gradient - involving, say, a small ionic species - by actively transporting this species out of the cell so that its concentration would be lower on the inside. This could balance transmembrane chemical potential differences so that there would be no net tendency for water to enter or leave the cell. We know that "modern" cells have integral membrane proteins that can act as ion pumps, given an energy supply in the form of ATP.
Whatever the earliest mechanisms for active transport may have been, they would have required the input of energy to generate and maintain the ionic concentration gradient.
Conversely, given that a concentration gradient across a membrane represents a form of free energy, it is in principle possible to utilize such gradients to drive the formation of ATP if a suitable gradient could be produced by a separate, independent process. Since many biochemical reactions involve the uptake and release of protons, it may have been easiest for ancestral cells to develop integral membrane "machinery" (i.e protein complexes) that could take up protons from the medium on the inside of the cell, while releasing them to the outside. Such molecular machinery could carry out energy-releasing "chain reactions" that provide the free energy to drive vectorial hydrogen ion transport.
Two major energy-harvesting processes in biochemistry - oxidative phosphorylation and photosynthesis - both create a "downhill" flow of electron transfer reactions that drive the formation of a transmembrane proton gradient. In the former case, the energy comes from oxidation of exogenously derived "food" molecules such as glucose, while in the latter case, sunlight is the ultimate source of energy.
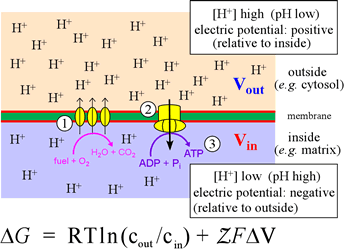
The figure at left illustrates oxidative phosphorylation in a summary cartoon. In the stepwise biochemical process of glucose oxidation to water and carbon dioxide, electrons are fed into the so-called electron transport chain. The three vertical ovals in this cartoon represent membrane-embedded protein complexes that carry out the electron transport chain, which couples electron flow, which to vectorial movement of hydrogen ions (Step 1, three upward arrows). This generates the free energy of an electrochemical gradient (specifically, a proton gradient, or a transmembrane ΔpH). The energy of this gradient is harvested when the H+ are allowed to move back across the membrane (Step 2) to drive the synthesis of ATP from ADP and phosphate (Step 3).
This is carried out in cells by a transmembrane protein complex called ATP synthase. In essence, the energy released by chemical reactions is transduced into a different form of potential energy associated with the physical separation of charged species across a membrane, a physicochemical form of energy. This energy is in turn transduced into the biochemical energy "currency", ATP.
The quantitative relation that holds for the free energy of a system in which a charged species exists at different concentrations on either side of an impermeable membrane is given by the equation, which has two terms. These correspond to concentration difference (or "gradient"; cout and cin are the activities of the species on either side) and a voltage (transmembrane electric potential difference) due to the charge imbalance associated with the chemical gradient. The quantity Z represents the charge on the species (+1 for the hydrogen ion), F is the Faraday constant, which in effect converts between energy units volts and kJ/mol (96.485 kJ/V·mol, or 23.061 kcal/V·mol). For H+, the side of the membrane with the higher concentration (lower pH) will be the more positive in electric potential. Thus, the two terms in the equation above (considering just H+), will have the same sign and add together to determine ΔG.