BIOCHEMISTRY TOPICS

Spectrophotometry

The electromagnetic (EM) spectrum and the properties of light. Absorption and emission of light. Transmittance, absorbance and Beer's law.

---

The interactions between matter and energy provide many fascinating and incisive windows into the nature of the molecules that make up all the substances around us. Many different instrumental techniques based on the interaction of matter with radiant energy have been developed that are employed in chemistry. A spectrophotometer is a type of instrument that can measure intensities of light within narrow bands of wavelength, and it is used in conjunction with chemical analysis, since with this instrument the interaction of various samples of different wavelengths of light can be measured. We undertake a survey of some common spectrophotometic techniques by beginning with a description of the electromagnetic spectrum.

The electromagnetic (EM) spectrum and the properties of light

The electromagnetic (EM) spectrum encompasses a wide range of types of radiation that are familiar to us in a variety of different contexts - radio waves, visible light, X-rays - but these are all fundamentally the same physical phenomenon. Visible light represents only a small portion of the entire EM spectrum. EM radiation propagates as waves, which have characteristic wavelengths (wavelength is symbolized as λ). As all EM waves travel at the same speed c in a vacuum, the following relationship between wavelength (λ) and frequency (ν) of electromagnetic radiation:

c  =  λν.

where c, the speed of light in vacuo is given by c = 2.9979246 × 10⁸ m/s).

While electromagnetic radiation can be described adequately as a wave in many contexts, in other respects - particularly where it concerns its interactions with matter on the nanoscale, that is at the level of individual atoms or molecules, EM radiation reveals a quantum nature. One of the key implications of this aspect of the dual nature of EM radiation is the following relation between energy and frequency (Einstein-Planck relation):

E  =  hν

The quantity h is Planck's constant, a fundamental constant of nature that corresponds to the quantization of matter and energy at the atomic scale. The value of Planck's constant: h = 6.6260688 × 10⁻³⁴ J s.

We can derive a relation between the energy and the wavelength of EM radiation by combining the above two relations. Substituting ν = c/λ into Planck's relation yields E = hc/λ. In spectrophotometry, the quantity wavenumber is sometimes used (symbolized ν-bar) which is defined as 1/λ . Thus, while wavelength is inversely-proportional to energy, both wavenumber and frequency are directly proportional to energy.

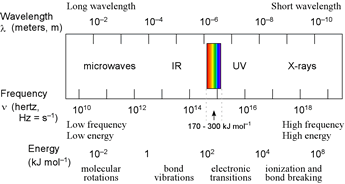
Left: Diagram of EM spectrum showing correspondence between energies and atomic and molecular transitions. In the interactions of EM radiation and matter, absorption and emission (described below) correspond to transitions between energy levels. Absorption of low energy EM radiation in the microwave range causes molecules to be promoted to a state with increased rotational energy. The intermediate energies of infrared (IR) radiation are associated with vibrational transitions in molecules. When atoms or molecules absorb higher energy radiation in the UV-visible range, an electron is promoted to a higher energy orbital, or (if the radiation is sufficiently energetic) completely separated from the atom or molecule (i.e. ionization). Loss of electrons due to ionizing radiation can lead to significant bond cleavage in molecules.

Absorption and emission of light

In order to understand spectroscopy and spectrophotometric methods, we need to first be acquainted with the nature of light's interactions with matter. At an atomic level, the quantized packets of light energy, known as photons, interact with individual atoms or molecules, often being absorbed. This process of absorption can occur only when the difference in molecular energy levels ΔE is matched by the energy carried by the photon -- that is, when ΔE = hν. When an atom or molecule absorbs a photon, it is thereby promoted to a higher energy or excited state. This excited state is usually extremely short-lived. Nonetheless, this absorbance by atoms or molecules is readily detected and measured (see below). A plot of absorbance measured at each given wavelength versus wavelength is an absorption spectrum.

Excitation and emission spectra. When atoms or molecules are promoted to a higher energy state, they subsequently emit light of only certain characteristic wavelengths, with the atom returning to its lower energy state. The process of putting energy into a collection of atoms or molecules is called excitation, while the pattern of characteristic wavelengths emitted by the atoms in response to excitation is called the emission spectrum of that atom or molecule. Atomic emission spectroscopy, which measures the emission spectrum of a population of excited atoms, is an important analytical method.

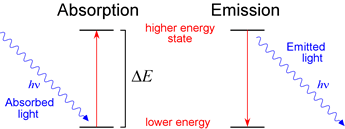
Absorption and emission. An atom in a lower energy state can absorb light of frequency ν and thereby be promoted to a higher energy state, provided hν = ΔE, where ΔE is the difference in energy between the two states of the atom. Emission is the reverse of this process

In atomic emission spectroscopy, discrete, narrow bands of atomic emission spectra (line spectra) are characteristic of atom type. Analysis of the emission of a from a sample excited in the laboratory can be used to determine amounts of different elements contained in the sample. Analysis of the light from the stars and distant nebula allows the detection of elements in other parts of the universe.

Transmittance, absorbance and Beer's law

A chromophore is a chemical species that strongly absorbs light, typically in the visible region. Any substance with a strong visible absorption will appear to us as colored. For instance, the green color of the leaves of trees and grass is due to the strong absorbance of chlorophyll in the red and blue regions of the visible spectrum. The remaining wavelengths, mostly in the green part of the spectrum are reflected or transmitted, and consequently leaves appear green to us. We have seen the description of what accounts for absorbance at the atomic and molecular scale. Let us return to consider the bulk, macroscale consequences of these nanoscale events. In an experiment where a monochromatic beam of light passes through a solution of a chromophore with concentration c, the intensity of incident light is compared to the intensity of transmitted light. If the wavelength of the incident light matches - in energy, via the Einstein-Planck relation - the energy gap of a molecular transition (in the UV-visible range, this would be an electronic transition in which an electron is promoted to a higher energy orbital), some of the photons of the incident light will be absorbed as they encounter chromophore molecules. In this case, the intensity of the transmitted light of this wavelength will be measurably less than the incident intensity.

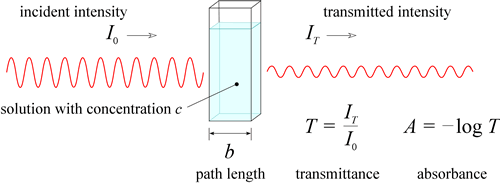
We would like to know the quantitative relation between concentration of the chromophore and this observable drop in transmittance, T, which is defined as the ratio of the transmitted intensity to the incident intensity. Clearly, transmittance and concentration are inversely related - as concentration goes up, transmittance should go down. Furthermore, the probability that a photon will be absorbed in an encounter with a chromophore molecule ought to be proportional to the length of the path the light beam travels through the solution, as well as the concentration of the chromophore in solution. As the probability that a photon will be absorbed as the light passes through the solution is increased, transmittance decreases, and absorbance, A, defined as − log T, increases. In fact, the relation between absorbance and the product of path length and concentration is a direct proportionality, a result that is known as Beer's Law (or the Beer-Lambert law).

A = εbc

In this equation, ε is an absorptivity coefficient the value of which depends on the nauture of the chromophore, the wavelength at which absorbance is measured, and the units of concentration and path length chosen. It is important to remember that while Beer's law is a general relation, it is specific to a given wavelength and chromophore.