Lecture 14. Chemical equations and stoichiometry
Tuesday 5 March 2024
Chemical equations as symbolic representations of a chemical change. Writing and balancing chemical equations. Reaction stoichiometry. The concepts of limiting reactant and theoretical yield. Combustion reactions. Solutions and solution stoichiometry. Molecular electrolytes: Acids, bases, and gases. Solutions: Concentration units and solution preparation. Solution stoichiometry. Solubility of ionic compounds and solubility rules. Aqueous reactions: Precipitation reactions. Representing aqueous reactions.
Reading: Tro NJ. Chemistry: Structure and Properties (3rd ed.) - Ch.7, §7.1-7.4 (pp.287-313).
Summary
We begin with a more formal description of chemical equations. A chemical equation is a symbolic representation of a chemical change or process. In the figure below, an example chemical equation is labelled according to its components. The set of species on the left side of the rightward arrow are called the reactants; those on the right side are the products. The italicized abbreviations in parentheses indicate the physical state of each species. The common phases of matter are designated (s), (l), (g) for solid, liquid, and gas, respectively.
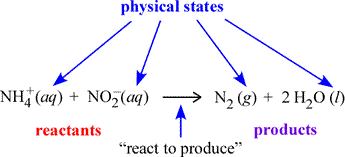
The (aq) seen at left designates a species dissolved in water to form what is called an aqueous solution. How we can translate, or read out, a chemical equation? Here, we could read the example equation as "an ammonium ion and a nitrite ion (in aqueous solution) react to produce one molecule of gaseous diatomic nitrogen and two molecules of water".
The above equation is balanced in that there are the same number of atoms of each type on the reactant and product sides, as required by the law of conservation of mass, which applies to chemical reactions. The act of balancing chemical equations - when initially in an unbalanced or skeletal form - is treated below.
The term "process" is more general than "chemical change", and we commonly use the symbolism of chemical equations to represent a variety of processes, e.g. physical changes:
H2O(l) → H2O(g)
We will in succeeding lectures, modify the basic chemical equation or add other features to indicate properties of the process it represents, such as energy changes and dynamic equilibrium. For now, bear in mind that the chemical equation is a symbolic language in chemistry that you ought to practice using at every opportunity. Mastering the symbolism is much like developing foreign language skills. One would not feel at home or be able to effectively interact with the society in a country speaking a different language without some fluency in that local language; so too understanding and using chemical equations will help you feel more at home in the world of chemistry. Many problems in chemistry are most clearly analyzed by writing the applicable chemical equations, and failure to do so often results in being led astray.
Balancing chemical equations is a skill best learned by practice. A redeeming feature of this type of problem is that carefully checking that your equation satisfies a simple criterion, you know whether or not you have the right answer. We refer to an unbalanced chemical equation as a skeletal equation. The skeletal equation is only a qualitative expression - it tells us what the reactants and products of a reaction are. It does not provide us with the quantitative, or stoichiometric relationship of the reactants and products. A balanced chemical equation satisfies the criterion that the number of atoms of each type of element is the same on both sides of the equation. That this must be true for a properly balanced chemical equation is a result of the law of conservation of mass.
Many chemical equations in their skeletal form can be easily balanced by inspection because of their relative simplicity. However, for more complex equations, a more systematic approach is advisable. The first principle of such an approach is to balance each atom type individually, and look at the equation to see how many formulas each atom type occurs in. One should start by balancing the atom type(s) that occur in the fewest number of formulas, and leave the atom type that occurs in the greatest number of formulas for last. Another principle to use to to recognize groupings of atoms in the formulas - such as polyatomic ions - that remain unchanged in the reaction, and treat them the same as if they were atoms.
Examples of balancing chemical equations
Example 1: Complete combustion of octane (C8H18).
Example 2: A second example.
Example 3: Balance the following skeletal chemical equation:
ClO2 + H2O → HClO3 + HCl
Solution: To balance any equation, we need to keep track of the numbers of atoms on each side, trying to use coefficients for the atoms and molecules involved so the numbers of each atom type are the same on both sides. This is an iterative bookkeeping process, and sometimes it may seem that we just have to try things until something works. First off, let's see where we stand with the reaction as it is written:
| atom | reactants | products | ClO2 + H2O → HClO3 + HCl Things look bright - there are three types of atoms to balance, and two of them are already balanced. But Cl is not balanced, and there is only one choice at this point: We must multiply the ClO2 species on the reactant side by 2 to bring the Cl atoms into balance. But this changes the number of O atoms. So we have: |
|||
| Cl | 1 | 2 | ||||
| H | 2 | 2 | ||||
| O | 3 | 3 | ||||
| atom | reactants | products | 2ClO2 + H2O → HClO3 + HCl Now H and Cl are both balanced, but we have a problem with O. But note that if we multiply the O-containing species on the reactant side by 3, and the O-containing species on the product side by 5, we should get the same number of O atoms on each side. We keep our fingers crossed in hopes that this doesn't throw anything else out of balance: |
|||
| Cl | 2 | 2 | ||||
| H | 2 | 2 | ||||
| O | 5 | 3 | ||||
| atom | reactants | products | 6ClO2 + 3H2O → 5HClO3 + HCl It worked! Our equation is balanced. It must always be possible to balance an equation representing any legitimate chemical reaction. |
|||
| Cl | 6 | 6 | ||||
| H | 6 | 6 | ||||
| O | 15 | 15 | ||||
Stoichiometry - the measure of the elements
We can distinguish two types of stoichiometry, namely formula stoichiometry, the proportions of the elements that make up the chemical formula of a compound, and reaction stoichiometry, the proportions of reactants and products represented by a balanced chemical reaction. The subscripts of the atom types in a chemical formula give the formula stoichiometry for the corresponding compound, while the leading coefficients in a balanced chemical equation (stoichiometric coefficients) give the reaction stoichiometry of the chemical reaction the equation represents.
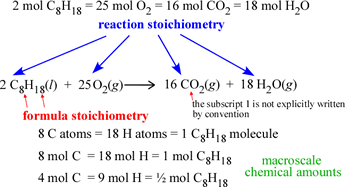
Note that the stoichiometric relations are equivalencies that yield chemical conversion factors. For example, if we consider the reaction shown at left, the equivalence of 1 mol C8H18 and 8 mol CO2 can be turned into two chemical conversion factors:
With the conversion factors derived from reaction stoichiometry, we can address problems such as the examples 7.4 and 7.5 presented in §7.4 of our text (Ref.1).
We'll next turn our attention to problems that utilize reaction stoichiometry. The principal type of problem we address involves determination of the limiting reactant. We will want to begin with a clear understanding of stoichiometric equivalence in a chemical reaction.
Example problem: How many grams water (H2O) are required to react with 56.5 grams of chlorine dioxide (ClO2) according to the balanced equation for the reaction involving chlorine dioxide and water as reactants, and hydrogen chlorate and hydrogen chloride as products?
Solution: We can state this problem as finding the stoichiometrically equivalent amount, in g, of the reactant water to the given mass of the other reactant, chlorine dioxide. The reaction under consideration, balanced, is;
6 ClO2 + 3 H2O → 5 HClO3 + HCl
We will need to convert the given mass of chlorine dioxide to moles, then use the stoichiometric relationships of the balanced chemical equation to relate mol ClO2 to mol H2O, then convert mol water to the mass of water in grams. The necessary formula masses are
67.45 g / mol ClO2 18.02 g / mol H2O
To construct the necessary stoichimetric conversion factor, use the equivalence relation (embedded in the balanced equation)
6 mol ClO2 = 3 mol H2O or more simply: 2 mol ClO2 = 1 mol H2O
This gives the conversion factor (1 mol H2O / 2 mol ClO2) for mol ClO2 → mol H2O, and the sequence of conversions
mass ClO2 → mol ClO2 → mol H2O → mass H2O
provides us the answer:
mass H2O
= (56.5 g ClO2 )(1 mol ClO2 / 67.45 g ClO2)(1 mol H2O / 2 mol ClO2)(18.02 g / mol H2O)
mass H2O = 7.55 g.
Let us pause for a moment to consider what this says. If we start with 56.5 g chlorine dioxide, then 7.55 g water is just sufficient to react with all the chlorine dioxide. In terms of mass, 7.55 g of water is stoichiometrically equivalent to 56.5 g chlorine dioxide. If the mass of water is less than 7.55 g, chlorine dioxide will be in stoichiometric excess, and water will be the limiting reactant. If the mass of water is greater than 7.55 g, then the 56.5 g chlorine dioxide will be limiting.
Limiting reactant and percentage yield
In practice, chemical reactions do not proceed with 100% efficiency, defined here as complete conversion of reactants - in stoichiometric proportion - to products. There are special measures that can be taken, however, to more completely convert a given reactant, one of which is to supply excess amounts of any other reactants that are participants in the reaction. This makes the given reactant the limiting reactant, with other reactants in stoichiometric excess.
With any reaction, we know how to calculate the mass of products, or theoretical yield, given the mass of the limiting reactant and assuming 100% conversion. Nonetheless, it is typical that less than 100% conversion of the limiting reactant is achieved, and this observed yield (or actual yield) divided by the theoretical yield leads to a quantity known as percent yield.
Example problem: What is the theoretical yield if the example reaction above is carried out starting with 5.00 g water and 56.0 g of ClO2? Which reactant is limiting?
Solutions
Much if not most of the chemistry we are concerned with occurs in solution. We need to learn the basic concepts and terminology of solutions. A solution is a homogeneous mixture of compounds, typically consisting of a major component called the solvent, and a minor species, designated the solute. When we think of solutions, we normally envision a liquid phase solvent, but the definition of a solution encompasses solid (e.g. metal alloys) and gaseous mixtures. Nonetheless, for the most part in this course we will consider aqueous solutions, that is solutions of compounds in which water is the solvent.
Electrolytes (musical accompaniment to this topic) are substances that create ionic species in aqueous solution. We can demonstrate the existence of charge carriers in solution by means of a simple experiment. The conductivity of aqueous media can be observed by using a pair of electrodes, connected to a voltage source, that we immerse in the solution. The current the solution conducts then can be readily measured; we use a light bulb as a visual indicator of the conductivity of a solution.
When this experiment is performed with pure water, the light bulb does not glow at all. Water itself does not conduct electricity easily; it is an example of a molecular substance that is a nonelectrolyte. For many other molecular substances, as solutes mixed with bulk water as solvent, the light bulb still does not light up. These molecular compounds apparently do not produce ions in any significant quantity as solutes in an aqueous solution. For example, table sugar (sucrose, C12H22O11) - is quite soluble in water, but a sugar solution apparently conducts electricity no better than just water alone. On the other hand, when we perform the experiment with a freely soluble ionic compound like sodium chloride, the light bulb glows brightly.
Let us represent what we think is going on with these contrasting cases of the dissolution of a molecular and an ionic compound by writing the following chemical equations:
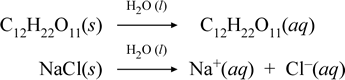
The first equation above represents the dissolution of a nonelectrolyte, the molecular compound sucrose. The second equation represents the dissolution of an ionic compound, sodium chloride. The key distinction between the two chemical equations in this case is the formation in the latter of aqueous ionic species as products. The ions are free to diffuse individually in a homogeneous mixture, and when a voltage is applied, the ions will move according to the electric potential energy difference between electrodes, thus carrying electric current. Note that water is not shown on the reactant side of these equations, but instead is shown above the arrow, indicating that water determines the environment in which the dissolution process occurs. The superstoichiometric status of water in this symbolism can be read as a dissolution process occurring with water as the solvent. We will not write water as a reactant in the formation of an aqueous solution by a simple dissolution process. There are many cases in which a substance reacts with water as it mixes with and dissolves in water. This reaction of a solute in aqueous solution gives rise to chemically distinct products. In such cases water can be explicitly shown in the chemical equation as a reactant species.
Solutions: Working with concentrations and stoichiometry
In any quantitative treatment of solutions in chemistry, it is necessary to define the intensive quantity of solution concentration. Concentration of solute at the nanoscale could be expressed as number of solute particles (atoms, molecules, or ions) out of total number of particles (solute + solvent). In the everyday or laboratory macroscale realm, concentration units based upon mass or chemical amounts per unit volume are defined. For example, in laboratory work accompanying this course, the mass-based concentration unit milligrams solute per milliliter of solution (mg/mL) is employed in spectrophotometric measurements of solution concentration. Subsequently, the concentration unit of molarity, based on chemical amount (mol), is introduced for applications involving solution stoichiometry.
There are two important practical applications of the use of solution concentration, which we pose as the following questions: (1) How does one prepare a solution of a given solute that has a specified concentration? (2) Once we have a solution of a given concentration, how can we produce a specified volume of solution of the same solute at a lower concentration?
The short answer to the first question is that either a recipe is available, or it becomes necessary to derive such a recipe based on the specifications of solute composition, amounting to a target solute concentration and solution volume. The amount of solute species to dissolve in enough solvent to make up the target solution volume V is given by its product with target solution concentration c:
c·V = amount of solute
The second question describes a process called dilution, and the builds on the above relation by noting the amount of solute remains constant for the second solution, hence the product of its decreased concentration and increased volume is equal to that of the first solution. This results in a formula used in determining how the dilution is to be performed a dilution calculation.
c1· V1 = c2· V2
Defining the concentration unit of molarity allows the expression of stoichiometric relationships in a chemical reaction taking place in solution by reactant solution volumes. Suppose there are two solutions, with solute species A and B, that undergo a reaction
a A + b B → products
with the reactants in balance according to their stoichiometric coefficients a and b. Then given two solutions, with solute concentrations [A] and [B] (square brackets are used as a notation for the molar concentration of the bracketed species), a specified volume of the solution A can be converted by calculation to the volume of the solution of B that would react completely with A when the two solutions are mixed. Another way to state this is that the two volumes are stoichiometrically equivalent. Note that it is assumed in this reaction-in-solution scenario that whatever A and B are present are 100% converted to products. This is known as theoretical yield of products.
More on solutions...