GENERAL CHEMISTRY TOPICS

Enthalpy

State functions and total internal energy. Enthalpy and thermochemistry. Enthalpy is a state function: Thermodynamic cycles. Standard state enthalpies, enthalpy of formation, and Hess's law.

---

Enthalpy: An important state function

We here introduce and define the enthalpy state function. In classical thermodynamics, the enthapy function is defined as a linear combination of the total internal energy state function E and the product of state variables pressure (P) and volume (V). The enthalpy function is also a state function and is quite useful because of the relationship ΔH = q_P, that is the change in enthalpy (ΔH) is equal to the heat exchange part of the change in total internal energy (ΔE) when the corresponding process is taking place within a system under conditions of constant pressure.

The second equation asserts that the change in enthalpy (ΔH_sys) is equal to the sum of change in internal energy (ΔE) and the change in the value of the product PV. If the condition of constant pressure is imposed, then this constant value can be factored out from the change in volume. Note that this latter term represents minus the pressure-volume work performed by the system. (Note that when we omit a subscript for thermodynamic values in this context we can assume they refer to the system is under consideration.)

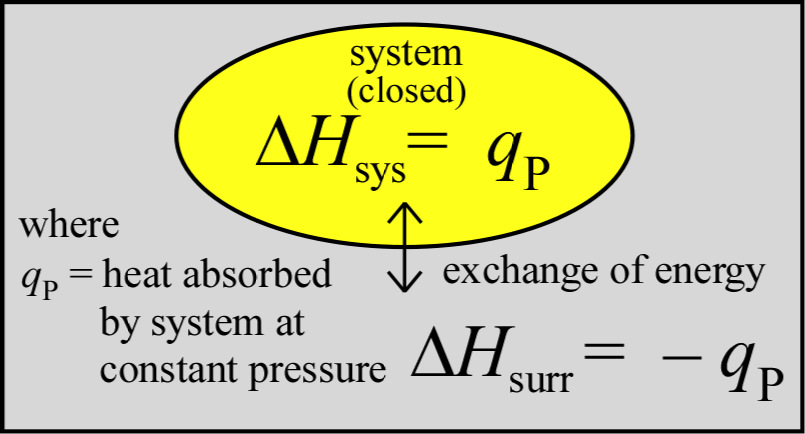
The important and useful relationship between the change in enthalpy (ΔH) and the heat (q) transfered to or from the system in a process provides a recipe for experimental mesurement of ΔH for a process. We can see that this relationship, ΔH_sys = q_P arises in the case where only PV work contributes to ΔE_sys. Using the definitions for both the latter, we can write

ΔH_sys = ΔE_sys + PΔV_sys

ΔH_sys = (q_{P, sys} + w_sys)   +   PΔV_sys

ΔH_sys = q_P − PΔV_sys + PΔV_sys   =   q_P

There are a number of important properties of state functions that we will use enthalpy to illustrate. There are equivalent ways in which the state function properties can be stated. Path-independence, thermodynamic cycles, and Hess' law are all direct consequences or applications of state functions.

 

Enthalpy is a state function: Path independence

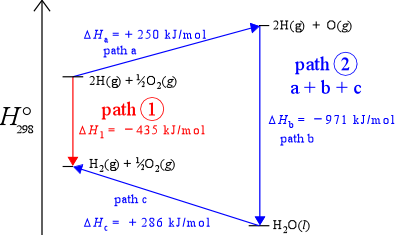
Path-independence means that no matter what path (sequence of changes in chemical compostion and other state variables) a system takes in going from state 1 to state 2, the change in value of the state function is the same. Another way of saying this is that the value of a state function is determined solely by its current state, not by its "history" (exactly how it got to that state). The figure below, an enthalpy diagram, which represents enthalpy changes along a vertical axis, illustrates the idea of path independence for the example of the formation of diatomic hydrogen. If we include oxygen in our system, we can imagine the same process occurring in the presence of oxygen. As long as oxygen remains unchanged, the enthalpy change for the reaction converting H atoms to H₂ molecules remains the same, – 435 kJ/mol (the downward red arrow in the figure). Given the presence of oxygen in the system, we can also imagine an alternate path - path 2 - connecting the two states (the three consecutive blue arrows - steps a, b,and c). The sum of the enthalpies for the three steps is – 435 kJ/mol, thus ΔH is the same for two different paths connecting the same two states. This is actually just another way of saying enthalpy is a state function.

Enthalpy is a state function: Thermodynamic cycles

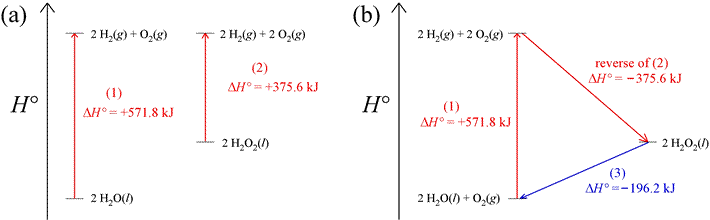
Since enthalpy is a state function, we can rely on the fact that there is no net change in its value for a cyclic process. In a cyclic process, the path followed is such that the initial and final states are the same. Thus, ΔH = 0 for a thermodynamic cycle. As an example of how this can be applied, consider two reactions conducted under standard conditions (more on this below) that produce hydrogen and oxygen gas, represented in the enthalpy diagrams below. In part (a) of the figure are enthalpy diagrams for the two reactions, showing the change in standard enthalpy, ΔH° for both. Part (b) illustrates how a thermodynamic cycle can be constructed by combining the first reation of (a),

2 H₂O(l) → 2 H₂(g) + O₂(g),

the reverse of the second reaction of (a),

2 H₂O(l) → 2 H₂(g) + O₂(g),

plus a third reaction, the decomposition of hydrogen peroxide to water and oxygen,

2 H₂O₂(l) → 2 H₂O(l) + O₂(g).

The standard enthalpy change for this last reaction can be computed because the changes in standard enthalpy, ΔH°₁ and ΔH°₂ are known, and ΔH°_cycle = 0. The cycle begins and ends with 2 mol water and 1 mol oxygen at standard state, as illustrated in the enthalpy diagram of part (b) of the figure. That the value of ΔH° for the reaction in which hydrogen peroxide is converted into water and oxygen can be directly calculated is illustrated in the enthalpy diagram.

Path-independnce and thermodynamic cycles, as presented in these two examples are different ways of looking at the same concept of a state function.

Enthalpy and thermochemistry

As a practical matter, we may be interested in the enthalpy changed associated with phase changes or chemical reaction. For example, the amount of heat produced from the combustion of various carbon-based fuels is relevant to the economics of heating indoor spaces. Defining the enthalpy of a system as H = E + PV means that H is a state function, since each of its components are also state functions. Defining the enthalpy is useful because of the relationship ΔH = q_P .

Since the enthalpy change of the system as a result of a process carried out at constant pressure is equal to the amount of heat q transferred - denoted as q_P - we can readily measure enthalpy changes for chemical reactions in solution under atomospheric pressure. We also see that for processess accompanied by small changes in volume, ΔH and ΔE are approximately equal. Generally speaking, differences between ΔH and ΔE are not significant unless gases are produced or consumed.

In order to more precisely compare emthalpy changes for different processes and reactions, so in chemical thermodynamics, a set of standard conditions is defined, and change in standard enthalpy, ΔH° is the enthalpy change when the reaction or process in general occurs under standard conditions. The use of standard reaction enthalpies is discussed further on the chemical thermodynamics page.