GENERAL CHEMISTRY TOPICS

Chemical thermodynamics

Thermochemical equations. Enthalpy of reaction. Using standard enthalpies of formation to calculate reaction enthalpies. Bond enthalpies and their use in estimation of reaction enthalpies.

---

The development of thermodynamics was intertwined the invention of the steam engine and the dawn of the industrial age. A practical aim of early thermodynamic studies was to maximize the efficiency of the steam engine. Ultimately, thermodynamics provides a precise characterization and deep theoretical understanding of heat and temperature. Later, application of its principles and theory to chemical phenomena in what we can call chemical thermodynamics, led to the accumulation of experimental data on energy changes associated with chemical reactions and the discovery of the laws that govern them. These laws allow us to predict which direction of a potential chemical reaction - its forward direction, or its reverse - will be favored under specified conditions, and what concentrations of reactants and products will be present at equilibrium.

Another matter of concern is the amount of heat released or absorbed by a chemical reaction occurring spontaneously under defined conditions. Typical examples involve combustion reactions including those familiar to us that are used to propel our vehicles and heat indoor spaces. If conditions specify constant pressure, the heat of reaction corresponds to its change in enthalpy, ΔH. This can be measured by calorimetry, here though we emphasize the use of thermochemical equations and compiled thermochemical data. The methods we illustrate below to determine the enthalpy change for a given chemical reaction are founded on the theoretical principle of enthalpy as a thermodynamic state function.

Thermochemical equations

A thermochemical equation is a balanced chemical equation plus one or more quantities representing the accompanying changes in thermodynamic functions per mole for the reaction as written. For example

H₂O(s) → H₂O(l)     ΔH = +6.01 kJ/mol

represents the thermochemical equation for the melting of ice. In general the thermochemical quantity (here enthalpy change, ΔH, for the process) is interpreted as an intensive quantity, thus 6.01 kJ of energy must be absorbed at constant pressure for every mole of H₂O(s) converted to the liquid phase. Very often, thermodynamic quantities are expressed as values measured under specified conditions, referred to as standard state. This is indicated symbolically using the degree (°) sign (for example, ΔH, the standard enthalpy change). Standard conditions are defined below.

Thermochemical equations can be manipulated, just like chemical equations, meaning we can multiply them by numerical factors and combine them together in various ways. The rules for doing so are mathematical in nature and preserve the correct stoichiometric relationships. In the case of thermochemical equations, the rules must also specify how the thermochemical quantities are treated.

Rules for manipulating thermochemical equations

• Multiplication by a factor n

  The stoichiometric coefficients and the thermodynamic quantity (ΔH) are both multiplied by n

  For n = −1, the chemical equation is reversed (products written as reactants, and vice-versa), and the thermodynamic quantity, (ΔH) changes sign.

• Adding equations

  The ΔH values are added (Hess's law), and species appearing on both sides of the equation can be canceled

Example: Combining thermochemical equations.

Given the following three thermochemical equations

H₂(g) → 2 H(g)     ΔH = +436.4 kJ/mol
Cl₂(g) → 2 Cl(g)     ΔH = +242.7 kJ/mol
HCl(g) → H(g) + Cl(g)     ΔH = +431.9 kJ/mol

find the value of ΔH for the reaction below:

H₂(g) + Cl₂(g) → 2 HCl(g)     ΔH = ?

Solution: The target reaction yields HCl(g) as products. In the given thermochemical equations, HCl(g) appears only as a reactant, in only one equation. This equation must be reversed. Furthermore, as there are 2 mol HCl(g) produced in the target reaction, this reversed equation must be multiplied by 2.

2 H(g) + 2 Cl(g) → 2 HCl(g)     ΔH = 2(−431.9) = −863.8 kJ/mol

To this, the other two thermochemical equations can be added to yield the target reaction. The figure below illustrates the addition of the three thermochemical equations, the resulting target chemical equation, and the corresponding addition of the changes in enthalpy ΔH values.

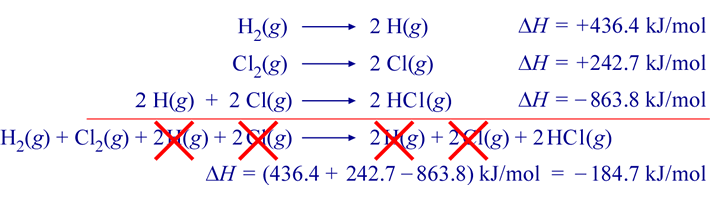
The resulting ΔH_rxn value for the target reaction is −184.7 kJ per mole (reaction as written). This manipulation of thermochemical equations is valid because of the fact that enthalpy is a thermodynamic state function. Specifically the implication that ΔH is path independent allows its calculation by summing ΔH values for any series of individual steps that lead from the initial state to the final state.

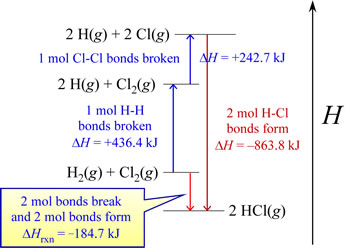
Another interpretation for this example comes to light via an enthalpy diagram. Such a diagram illustrates enthalpy changes for various processes along a single dimension. Increases in enthalpy (positive ΔH, endothermic processes) can be shown as upward arrows along a vertical axis, while decreases in enthalpy (negative ΔH, exothermic processes) are represented as downward arrows. The net enthalpy change for a multistep process is the sum of the upward and downward arrows. This is exactly the same as the enthalpy change for an equivalent overall process occurring via a single step, which diagrammatically represents what is referred to as Hess's law.

Standard enthalpies of formation and their use

Thermodynamic quantities known as standard enthalpies of formation have been measured for a great many compounds and are used in a procedure to calculate the enthalpy of any reaction involving these compounds. The standard enthalpy of formation (ΔH°_f) of a compound is defined as the heat absorbed or released when one mole of the compound is formed from its elements in their most stable states. The temperature is usually specified as 298 K. The standard enthalpy of formation of the most stable form of an element at the specified temperature is zero by definition. ΔH°_f  values are usually found in an appendix of a general chemistry textbook.

The procedure to calculate the standard enthalpy change (ΔH°_rxn) for a generalized chemical reaction,

aA + bB + cC + ····   →   xX + yY + zZ + ····

is to combine the ΔH°_f  values for the products and reactants according to the formula

ΔH°_rxn  =  x ΔH°_{f, X}  +  y ΔH°_{f, Y}  +  z ΔH°_{f, Z}  + ····    − a ΔH°_{f, A}  −  b ΔH°_{f, B}  −  c ΔH°_{f, C}  −  ····

This formula, based on the principle of Hess's law, is sometimes referred to as Hess's law equation. It should be noted that the stoichiometric coefficient could be interpreted as introducing the unit mol to each of the ΔH°_f  values, given in kJ mol⁻¹, so that the ΔH°_rxn  we compute is an extensive quantity. Alternatively, we can interpret the value intensively (keeping the stoichiometric coefficients unitless) as the amount of heat released or absorbed per mol of the reaction as written.

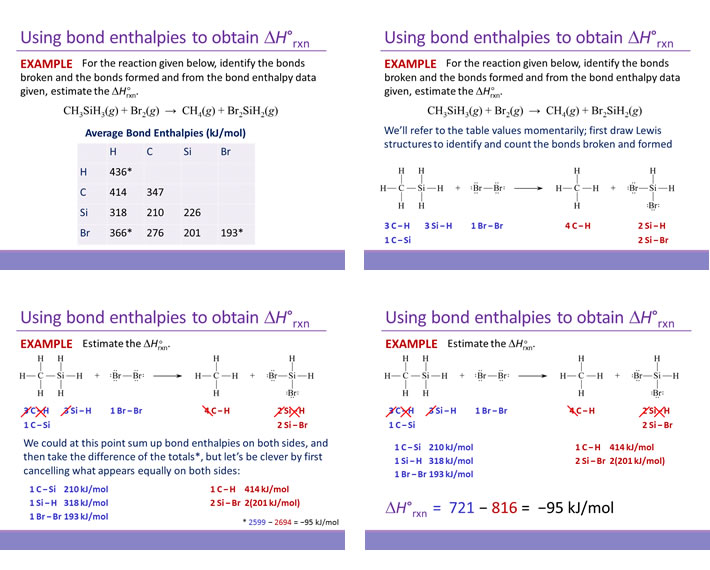
Bond enthalpy

Bond enthalpy is the enthalpy change associated with breaking a particular bond in 1 mol of gas-phase molecules. By convention, bond enthalpies are reported as positive values, corresponding to the endothermic process of bond breakage. Bond enthalpies (or bond energies) tabulated for common types of bonds can be used to estimate the enthalpy change of many different reactions. Note that only for diatomic molecules can the values be determined exactly. For polyatomic molecules, bond enthalpies are average values.

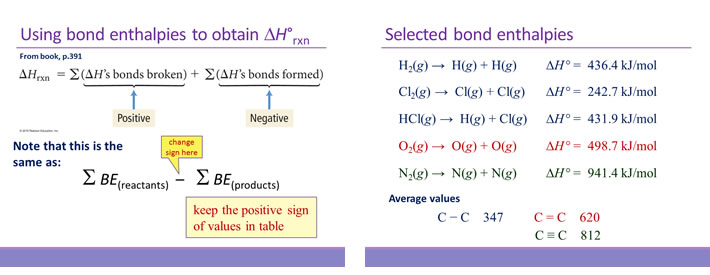
In using bond enthalpies to estimate a ΔH°_rxn, the procedure is to sum all the bond enthalpies of reactants and subtract from this the sum of all the bond enthalpies of the products.