GENERAL CHEMISTRY TOPICS
Gases and the ideal gas law
Introduction to gases. State of a system and state variables, revisited. The simple, or binary gas laws. The ideal gas law. Dalton's law of partial pressures.
Summary
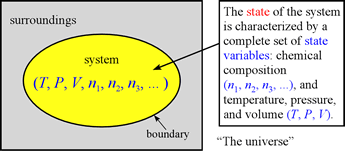
We have already been introduced in this course to the concept of state variables, and that the state of a system can be completely described by specifying values for the set of state variables P, V, T, n1, n2, ....
The values of these state variables are not all independent. The molar amounts of pure substances in a system undergoing chemical reaction will be related by the reaction stoichiometry represented in the balanced chemical equation for the reaction. Furthermore, as we will see in our treatment of gases, the study of gases revealed various relationships among the state variables in the absence of chemical reaction. The combination of all the state variable relationships into a single expression, the ideal gas equation, or ideal gas law, is an example of what is generally referred to as an equation of state. One can build up to the ideal gas law by first considering pairwise state variable relationships, the simple gas laws, thence to an equation relating P, V, and T, called the combined gas law.
We also treat the case of gas mixtures, introducing and applying the quantity partial pressure, which is defined for each chemically distinct component of a mixture of gases, such as the earth's atmosphere.
Important definitions and units
SI Unit for pressure:
Pascal (Pa) 1 Pa = 1 kg·m−1·s−2
= 1 N·m−2
(1 bar = 105 Pa = 100 kPa)
Other pressure units:
1 atm = 760 torr (exactly) =
1.01325 × 105 Pa = 101.325 kPa
Gas constant:
R = NAk =
8.31451 × 104 J·K−1·mol−1
= 8.20578 × 10−2 L·atm·K−1
·mol−1
The simple gas laws
A consideration of the study of matter that culminated in the ideal gas law is instructive for our understanding of the state variables it relates and their measurement. It is also an opportunity to reflect further on the nature of scientific investigation, and its historical development.

The first of the so-called simple gas laws to be established was what is known as Boyle's Law, attributed to Robert Boyle's work published in 1662. Boyle, born in County Waterford, Ireland to the first Earl of Cork, performed meticulously documented experiments and was a strong proponent of the methodology of experimental science, based on careful measurements and reproducible results. A contemporary of Isaac Newton, his work was carried out at Oxford, in England, where he worked with Robert Hooke, who has his own law regarding the force of springs.
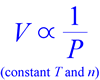
Boyle and Hooke performed experiments with the earliest air pumps in an attempt to create a vacuum - a radical pursuit - and the data they produced showed that as the pressure of a gas sample is decreased, its volume increases, such that - provided a constant temperature is maintained - the product of pressure and volume is constant. In other words, pressure and volume are inversely proportional.
Charles's law states that for a fixed amount of gas kept at a constant temperature, the volume of the gas is directly proportional to its temperature. This brings into question just what temperature is and how it can be measured. Charles's Law actually suggests the basic idea for measuring temperature. We have all experienced the expansion of substances with increasing temperature, and the classic mercury or alcohol-based thermometers measure temperature by height of a column of these liquids within an evacuated capillary. Charles's law suggests we could measure temperature by measuring the volume of an ideal gas, a so-called ideal gas thermometer. What a thermometer is actually measuring becomes more clear when we consider an ideal gas from the viewpoint of kinetic molecular theory
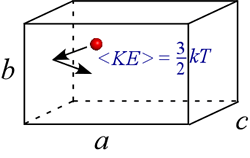
We can think of pressure as resulting from the innumerable collisions of the gas molecules with the walls of the container. The more molecules in the container, the higher the pressure of gas in a fixed volume at constant temperature. However, the pressure will also increase if the speed of the molecules increases for fixed number of molecules in a fixed volume. This is because molecules of a given mass colliding with the container walls will exert a greater force of collision if they are traveling faster on average.
This is in fact the meaning of temperature: it is a statistical result of a super-astronomical number of nanoscale particles (imagine the above pictured particle multiplied by a factor on the order of Avogadro's number), and the temperature of a system can be defined as a quantity proportional to the average kinetic energy, <KE>, of the atoms or molecules that make up a system.
We can also interpret Charles's law from this viewpoint, since if we increase the temperature of a gas contained in a cylinder with a movable piston that exerts a fixed pressure Pext on the gas, the volume will increase as the increased kinetic energy exerts a greater pressure than Pext. This imbalance of force moves the piston outward until the volume has increased enough to reduce the collision frequency to the point where Pint = Pext.
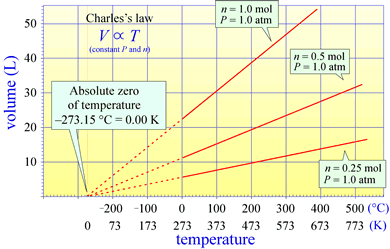
Charles's law is notable in that in the extrapolation of the relationship of volume to temperature for a fixed amount of gas at constant pressure suggests a temperature scale for which the zero temperature occurs at theoretical minimum (extrapolation to zero volume). This is the absolute zero, and a scale for which zero is set at this absolute zero and the size of a temperature unit, or "degree" is the same as that for the Celsius scale is the Kelvin, or absolute temperature scale. The statement of Charles's law actually implies an absolute temperature scale (one that goes to zero at absolute zero).
Avogadro's Law states that the volume of a gas is proportional to the number of moles of the gas (at fixed temperature and pressure).
Avogadro's law was a crucial advance toward correct formulas for simple compounds in the gas phase based on the law of definite proportions and Dalton's atomic theory. For example, it was known that water is composed of 1 g of hydrogen for every 8 g oxygen. This could imply a molecular formula for water of HO with the oxygen atom being eight times the mass of hydrogen. Alternatively, a formula of H2O would be implied assuming oxygen is 16 times heavier than hydrogen. We know the latter to be correct, but in Avogadro's time there was no way to either establish relative atomic masses (which would determine molecular formulas), or to establish molecular formulas for some simple compounds (which would then set a relative scale for atomic masses.) Avogadro's insight was to propose that equal volumes of gases at the same temperature and pressure contained equal numbers of particles (atoms or molecules) - a proposal that we recognize as equivalent to Avogadro's Law, but at the time it was known as Avogadro's hypothesis. Then, upon observation that two volumes of hydrogen gas combine with one volume of oxygen gas to produce two volumes of water in the gas state, which led to the correct formulas for hydrogen (H2), oxygen (O2), and water, as well as the correct relative masses of the atoms.
This simple gas law, when applied to reactions with gas-phase reactants or products translates reaction stoichiometry into gas volumes: Equal volumes of gases at the same temperature and pressure contain equal numbers of molecules or mol of gas
The ideal gas law
All of the simple gas laws can be captured in a single equation involving the state variables called the ideal gas law:
PV = nRT
where R is an experimentally determined constant of nature. Its value of course depends as well on the units we choose for the choose for the state variables. In particular, we have seen a number of different units are employed in measuring pressure. We will frequently use the value of 0.082057 L atm mol–1 K–1, but it is best to bear in mind that alternative values of R are used in other applications.
Standard temperature and pressure (STP)
It is convenient to define a standard temperature and pressure (STP) for gases. The standard temperature is 273.15 K, and standard pressure can be defined as 1 atm, exactly. This in turn is used to define a standard molar volume, the volume occupied by one mole ideal gas under conditions of STP.
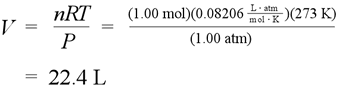
The calculation for standard molar volume (3 sig figs) for an ideal gas. With Avogadro's Law, the constant ratio of chemical amount (mol) to volume for any ideal gas at STP is set by this value.
Mole fractions and partial pressures in gas mixtures
Consider a mixture of gases, for example a dry sample of the atmosphere, which is about 78% nitrogen, 21% oxygen, 0.9% argon, and 0.1% a collection of trace gases. The total number of moles of gas in a mixture is the sum of the moles of each gas:
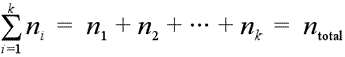
Equation showing total moles is a summation of moles of each component.
A general notation for summation is used, the Σ notation, which says to take the sum of a series of numbers, with index i, starting with i = 1 and continuing through i = k. In addition to a list of numbers, each with a label, or index, the ni can be used to represent expressions, the value of which depend on the value of the index i.
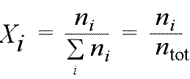
Equation for mole fraction. We abbreviate the summation symbol, at times omitting parts of the notation when the context allows it.
Dalton's law of partial pressures. Partial pressure is defined as the pressure a gas component in a gaseous mixture would exert if it were the only component in the volume occupied by the complete mixture. Provided we can treat the each component as an ideal gas, we can write the partial pressure for each gas according to the ideal gas law, resulting in the set of relations (1). When we sum all these partial pressures together (2), we find we can remove the common factor RT/V, as in (3), and thereby relate the sum of the partial pressures to the total chemical amount of gas, ntotal.
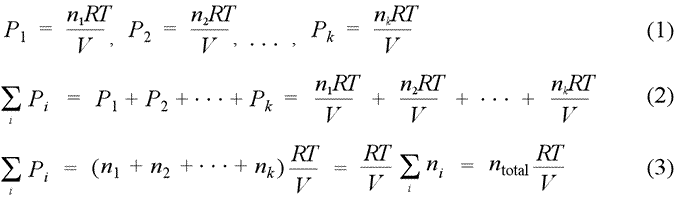
Dalton's law of partial pressures states that the total pressure of a mixture of gases equals the sum of the partial pressures of the component gases, that is, the ΣPi = Ptotal. We see from eq.(3) above that a gas mixture that obeys Dalton's law of partial pressures obeys the ideal gas law with the total number of moles, ntotal.
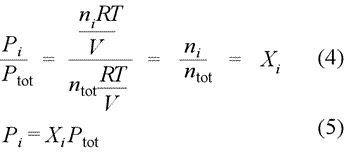
We can restate Dalton's law of partial pressures in terms of mole fractions, as defined above. If we divide the partial pressure of gas i by total pressure, as in eq.(4) below, we obtain the result [eq.(5)] that the partial pressure of gas i (component i of the gas mixture) is simply the total pressure times the mole fraction of component i.
Connections and further explorations
An advanced topic that treats explicitly an ideal gas as tiny particles behaving according to the laws of Newtonian mechanics, and actually leads to a derivation of the ideal gas law is referred to as kinetic molecular theory.
The ideal gas law assumes there are no interactions (forces acting between) the particles that make up an ideal gas, other than purely elastic collisions. In other words, that there are no intermolecular forces that would make atomic surfaces "sticky" at close range. Furthermore, the treatment of a gas as ideal assumes the total volume of the particles making it up are negligible. Corrections to the ideal gas law to account for these and other deviations from ideality include the van der Waals and virial equations.