GENERAL CHEMISTRY TOPICS
Resonance
When not just one Lewis structure will do. Resonance structures: Alternative Lewis structures as contributors to a hybrid. Resonance energy: A resonance hybrid has the lowest energy electron configuration. Examples of equivalent and nonequivalent resonance forms. Evaluating contributions of nonequivalent resonance forms to the resonance hybrid.
Summary
It is often the case that in drawing Lewis structures for the same arrangement of atoms, or skeletal structure of the molecule or ion, that there is more than one way to draw a valid structure. For example, two forms of the acetate ion can be drawn, depending on which oxygen forms a double bond and which oxygen is making a single bond to the same carbon and bearing the negative formal charge. It is important to note that the two forms differ only in the arrangement of electrons, not in the positions of the atoms (plus their core electrons).
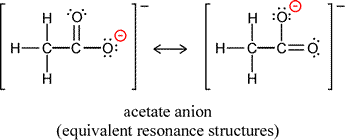
Does this matter? It would seem there is no basis to prefer one or the other of the structures. Can we just say either is correct and represents a good symbolic description of the acetate ion? Is the ion oscillating back and forth between the two structures? There is a further possibility, one that arises from quantum mechanics. Note that our Lewis structures do not depend on quantum mechanics, but stem from the octet rule and the covalent bond as a shared electon pair between two atoms. If we think of electrons in molecules and polyatomic ions quantum mechanically as waveforms, by analogy to atomic orbitals the electrons will occupy molecular orbitals. There would be no requirement for these orbitals to have significant electron probability density around only a single atom or pair of atoms. We might ultimately want to know what the sizes and shapes of such molecular orbitals would be, and certainly would want to determine the lowest energy arrangement of the electons in these orbitals, the ground state molecular electron configuration.
Developing this molecular orbital approach would take us a little deeper into theory than we are prepared for in this course, but let's adopt the concept that electrons in molecules and polyatomic ions occupy molecular orbitals. Our Lewis structures are in some cases inadequate representations of these. In the majority of cases we have encountered initially, putting valence electrons into two types of "orbitals", a shared pair of electrons between two atoms occupy a single bond orbital, and lone pairs or unpaired electrons reside in unshared, or nonbonding orbitals localized to individual atoms. What we need at this point is to allow for a type of molecular orbital that is delocalized, or more spread out among the atomic centers than the shared pairs that we so far have been treating as solely responsible for covalent bonding.

A delocalized molecular orbital is in fact present in the acetate ion, and this is the correct way to interpret the two equivalent Lewis structures that can be drawn. The term resonance refers to this situation, and each member of any set of valid Lewis structures is called a resonance form. The delocalized molecular orbital(s) will arise, in our conceptualization, by a combining of the resonance forms into a resonance hybrid. In the case of acetate, the resonance hybrid is the result of equal contributions from the two equivalent resonance forms. We can represent this symbolically by replacing the two resonance forms of acetate with a single structure that shows a dashed line bridging the three atoms involved in the differing arrangements of bonding and nonbonding electrons of the former.
What is the significance of the resonance hybrid beyond the idea that delocalization is a more accurate way to represent the actual distribution of electrons? What experimental evidence might support the existence and role of a delocalized molecular orbital in a resonance hybrid structure? To address these questions, we first note that all chemical species exist in general in their lowest energy states. This energy minimizing principle, when applied to molecular electronic distributions is manifested as a significant stabilization of the resonance hybrid. Furthermore, this resonance stablization energy is explained by the delocalization of a bonding molecular orbital. The spreading out of electron density through a larger volume lowers its energy, like a longer guitar string vibrates at a lower frequency. We could use the principle of minimizing energy as Linus Pauling did in his classic treatise The Nature of the Chemical Bond to define the real species that the resonance hybrid is supposed to represent as the quantum state of the molecule specifying an electronic distribution that gives the minimum possible energy. If we consider the resonance forms represented in our regular Lewis structures as possible quantum states, we find that their energy is not the minimum possible. In fact they have equal energies, an energy higher than a linear combination of the two states. The combination in which each makes an equal contribution (50% each) is indeed the minimum energy.
Experimental studies of the structure of acetate ion show that the two C-O bonds in acetate are equal in length. Furthermore this bond length is intermediate between the typical lengths of a pure C-O single bond and a pure C=O double bond. We explain this with the delocalized molecular orbital, which contributes half of a covalent bond to each carbon-oxygen bond, so that the bond order for these bonds is 1½. Other evidence points to the lower energy of the resonance hybrid state of acetate, such as the much greater acidity of acetic acid and other carboxylic acids compared to alcohols such as ethanol, for which no resonance stabilization occurs for the anion produced upon loss of H+.
Nonequivalent resonance forms
For the acetate example above, we dealt with resonance forms that were equivalent. This means that the description of covalent bonding, nonbonding electrons, and formal charges are the same. For acetate, both forms had a methyl group (the pattern of a carbon with three single bonds to hydrogen atoms, and an extra covalent bond available) bonded to a second carbon atom, which in turn forms bonds to two oxygen atoms, one by a double bond and with two lone pairs on the oxygen, the other by a single bond, this oxygen bearing three lone pairs and a minus 1 formal charge. Now consider the case of dinitrogen monoxide (nitrous oxide, N2O). With one of the nitrogen atoms central and 16 valence electrons, the Lewis structures shown in the figure can be drawn.
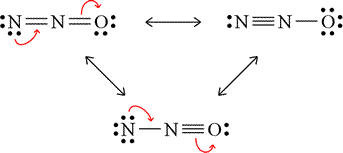
These three valid Lewis structures for dinitrogen monoxide are termed nonequivalent resonance structures. Note the different descriptions for each of the resonance forms, the number of bonds between which atoms and the number of lone pairs and formal charges of the atoms differing for each case. We might ask how nonequivalent resonance forms contribute to a resonance hybrid, and for this we'll lean on a qualitative approach to estimate this. Here there is a contrast to the case for equivalent resonance forms for which each would contribute equally to the hybrid since they are all equal in energy. Nonequivalent resonance forms will generally have different energies, and would therefore contribute to the hybrid differently, presumably according to their relative energies, the lower energy resonance form(s) contributing a greater proportion. As an assessment tool, formal charge assignments can be used to predict the relative contributions of the resonance forms to the resonance hybrid. The general rules for this will be first that strucures with no non-zero formal charges are lower in energy than those where formal charges are present, and then where non-zero formal charges are present, stictures with negative formal charges on the more electronegative atom(s) and positive formal charges carried by less electronegative atoms sre lower in energy than those where the opposite is the case.