Lecture 22. Equilibrium calculations
Tuesday 16 April 2024
Calculation of equilibrium concentrations. General procedures: The "ICE" table. Applying the quadratic equation to solve for equilibrium concentrations. Simplifying approximations.
Reading: Tro NJ. Chemistry: Structure and Properties (3rd ed.) - Ch.15 §15.5-§15.9 (pp.676-699).
Summary
To proceed further with a study of chemical equilibrium, we'll want to develop a quantitative description of equilibrium. This is extremely useful, as systems at equilibrium at a given fixed temperature are characterized by constancy in the values of reactant and product concentrations. We first construct an expression based upon the quotient of product to reactant concentrations, properly accounting for reaction stoichiometry, which we call the reaction quotient, Q. This allows us to formulate a law of equilibrium describing the finding that for a fixed-temperature system at equilibrium, there is a characteristic value of Q, called the equilibrium constant, Keq. We'll need to learn the rules for writing the reaction quotient expression given a complete chemical equation for a reaction. Once we are able to properly construct an expression for Q from any given chemical reaction, calculating the equilibrium constant from measured equilibrium concentrations is relatively easy. The same operation is involved in Q vs. Keq analysis to predict direction of change in a system capable of undergoing chemical change which is not at equilibrium. This method for predicting reaction direction is essentially a quantitative version of some of the applications of Le Châtelier's Principle.
Quantitative descriptions of equilibrium
For the generalized chemical reaction,
aA + bB = cC + dD
the reaction quotient expression, Q is given as
Q = [A]−a[B]−b[C]c[D]d
We will need to be more specific later about the phases of all reactants and products in the reaction equation, and how this affects the treatment of the terms in the expression for Q, but the key distinguishing feature of the terms [A], [B], etc., is that they represent intensive quantities proportional to the moles per unit volume, or concentration, of the species A, B, etc,. and that the value of these concentration terms changes in the course of a reaction.
When a chemical reaction occurs and reaches a state of equilibrium, the concentrations of the reactants and products no longer change with time. Thus for the chemical system at equilibrium, it is found that the value of the variable expression Q is constant with time. The equilibrium constant (Keq) is defined as
Keq = [A]eq−a [B]eq−b [C]eqc [D]eqd
where [A]eq, [B]eq, etc., are a set of values of [A], [B], etc., occurring when a state of equilibrium pertains. The magnitude of the equilibrium constant (Keq) determines the extent to which a reaction proceeds from reactants to products. There are three important general types of questions about chemical reactions that equilibrium constants can be used to answer:
- When equilibrium has been attained, do reactants or products predominate?
- Given initial concentrations of reactants and products, in which direction will the reaction go? ( Q vs. Keq analysis).
- Given initial concentrations, what concentrations of reactants and products are present at equilibrium?
The first two questions can be tackled straightaway. We will devote a subsequent lecture to the treatment of the third question.
Conditions at equilibrium
The magnitude of the equilibrium constant for a given reaction or process indicates whether the conditions prevailing at equilibrium favors reactants or products or whether there is a balance between the two.
Example
Consider the homogeneous gas phase reaction introduced last time
H2(g) + I2(g) = 2HI(g)
The reaction quotient expression is
Q = [HI]2 / [H2] [I2]
and the expression for the equilibrium constant takes on the same form
Keq = [HI]eq2 / [H2]eq [I2]eq = 50 (440 °C)
where the experimentally determined value of the equilibrium constant is given. The value shows that at equilibrium, the product, HI, is favored. Note that the number of moles of gas does not change in this particular reaction. For a total of 1.00 mol of a gas mixture initially containing HI, plus H2 and I2 in equimolar amounts, in a volume of 1.00 L, at equilibrium there will be 0.78 mol HI and 0.11 mol each of H2 and I2, since
(0.78)2 / (0.11)(0.11) = 50.3
that is, those amounts satisfy the equilibrium constant expression.
Q vs. Keq analysis
As we have seen, the expression for the reaction quotient Q has the same form as that for the equilibrium constant Keq. The crucial difference between the two is that while the value of Keq is fixed for a given temperature, and only a restricted set of concentrations of reactants and products satisfy the equilibrium condition, the value of Q can be any positive real number, and is simply the value given when concentrations of reactants and products take on arbitrary values.
We can compare the value of Q with that of Keq and thereby predict which direction the reaction will proceed in order to attain equilibrium.
For example, if the concentrations in the gas phase reaction
H2(g) + I2(g) = 2 HI(g)
are 0.02 mol HI and 0.49 mol each of H2 and I2, in a volume of 1.00 L, then the reaction quotient expression yields
Q = [HI]2 / [H2] [I2] = (0.02)2 / (0.49)(0.49) = 1.7 × 10−3
and Q < Keq so that to attain equilibrium, much of the H2 and I2 must be converted to HI. Alternatively, with the amounts 0.86 mol HI, 0.09 mol H2 and 0.05 mol I2, Q computes to about 1.6 × 102, so that Q > Keq and some of the HI must decompose for equilibrium to be established.
This type of analysis by comparison of Q and Keq can be represented on a graph of chemical potential energy versus composition of a reacting system, as shown below.
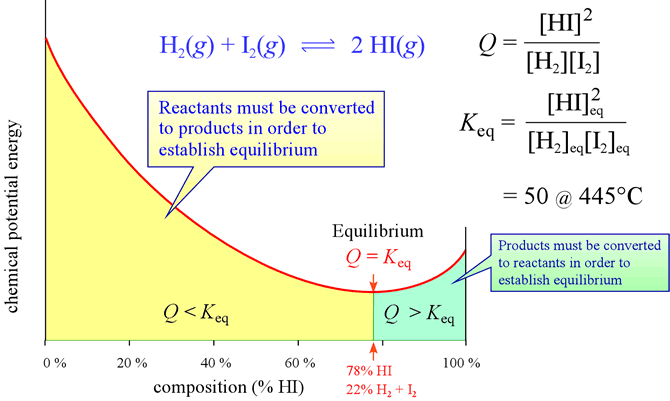
Above: Diagram showing the dependence of chemical potential energy on composition for the case of the reaction between hydrogen gas and iodine gas (reactants), and hydrogen iodide gas (products). Equilibrium corresponds to the minimum of chemical potential energy for this system, which is a function of both enthalpy and entropy.