GENERAL CHEMISTRY TOPICS

Entropy

Nature's tendency become more dispersed. Spontaneity and thermodynamically spontaneous processes. Definitions of entropy. The second law of thermodynamics.

---

Entropy: A measure of the dispersal of matter and energy

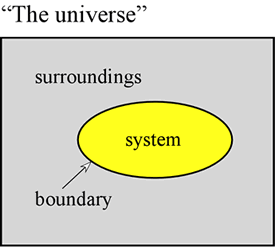
In looking for an answer to the question of what makes a process spontaneous, the thermodynamic approach examines processes by defining the system in which the process takes place, and characterize the process in terms of the change in the state of the system. A fundamentally important thermodynamic concept is that of a state function. Examples of state functions are total internal energy (E), enthalpy (H), and state variables (P, V, T, n). The first law of thermodynamics states that for any process,

ΔE_sys +  ΔE_surr  =  ΔE_univ  =  0

An examination of many processes seems to suggest that ΔE_sys or ΔH_sys < 0 for a spontaneous process. However, although this indeed turns out to be an important factor, we can nonetheless observe spontaneous processes for which ΔH_sys > 0 - the demonstration of the spontaneous - and endothermic - dissolution of ammonium nitrate in water is a case in point. We thus know that an application of the first law of thermodynamics is insufficient - something more is needed. The key to a criterion for spontaneity is provided by another state function called entropy (symbolized as S).

The definition of entropy paves the way for the second law of thermodynamics, which states that in any real (spontaneous) process, the entropy of the universe must increase (ΔS_univ > 0). This turns out to be the criterion for a spontaneous process. Furthermore entropy must figure in somehow in a definition of chemical potential energy.

There are two distinct ways in which entropy is defined, one based in statistical mechanics, the other founded on classical thermodynamics. Given the statement of the second law of thermodynamics above, it would seem important to be able to compute ΔS - for both the system and surroundings - for a process (such as a phase change or a chemical reaction). Then the second law of thermodynamics can be applied to determine whether the process is spontaneous.

Spontaneity and thermodynamically spontaneous processes

When we speak of a process, we are describing the transition of a system from one set of values for the state variables of a system to a different set of values. The reverse of such a process is the opposite change in state variables. Generally speaking, one direction of change, either the "forward" or the reverse process will tend to occur while the other is not observed. The observed direction of a process is called the spontaneous direction and constitutes what we call a spontaneous process, and its unobserved opposite is the nonspontaneous direction. Let's look at some examples and define more carefully the thermodynamic meaning of spontaneity. The first example is the transfer of heat between two blocks of substance initially at different temperatures and in thermal contact with each other. It is convenient here to define the system as the two blocks, and the surroundings as a perfect insulator so that there is no loss or gain of heat to the surroundings. Based on our experience we would predict that the warmer block would lose heat to the cooler until each reached a uniform in-between temperature. Recalling our study of calorimetry, we could further predict the final temperature given the initial temperatures and total heat capacities of the two blocks. But the main point here is that our assessment of the spontaneous direction is based on the observation that heat energy flows from warmer to cooler objects, never in the reverse. In this case, the process on which the system is specified as the two blocks initially both at the same temperature and end up at different temperatures is not observed. Now to be clear, we could observe this change of state in our system, but it would require energy transfer from the surroundings. Without intervention from outside the system, the transfer of heat from hot to cold is spontaneous. The reverse, transfer of heat from cold to hot, making cold cooler and hot hotter is nonspontaneous. In this sense, a spontaneous process is said to be irreversible.

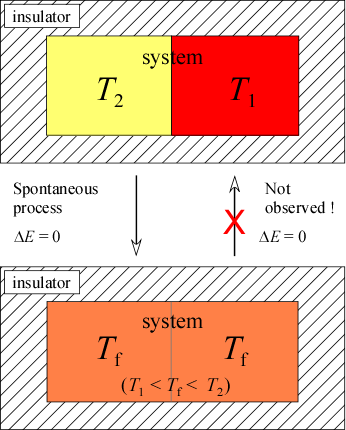
The first law does not help us in this case to decide which direction is spontaneous. No energy is lost or gained by the system. Only the way in which this energy is distributed changes here. How might the way in which energy is distributed serve as criterion for spontaneity? Note that in the initial state we can think of the internal energy corresponding to heat as being more concentrated in part of the system, and the final state is one in which energy is equally and uniformly distributed. This final state is called thermal equilibrium, and approach to thermal equilibrium will always be a spontaneous process. More generally, the idea of the distribution of energy from more to less concentrated, its being more spread out, as a feature of spontaneous processes turns out to be quite fruitful.

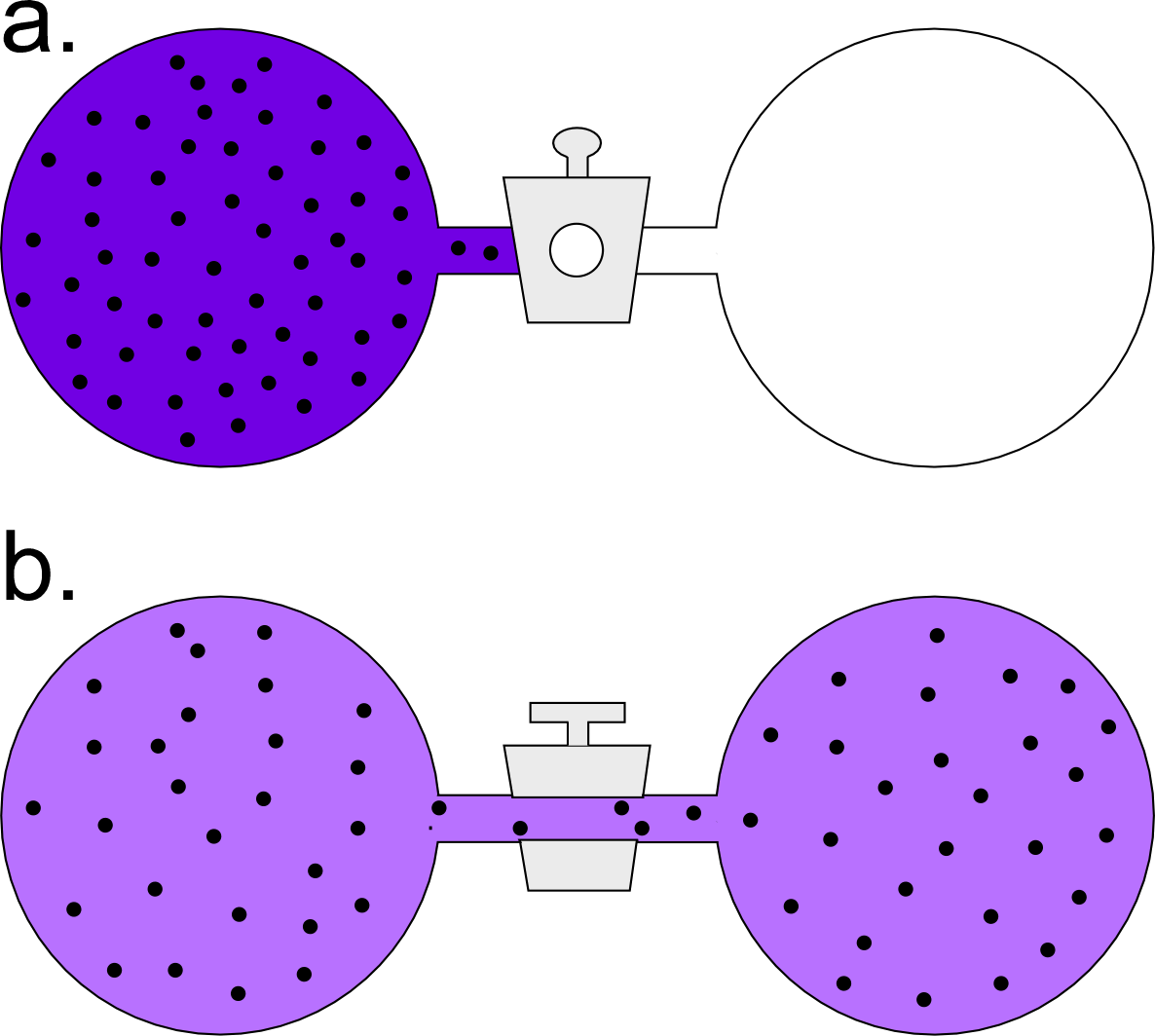
Our second example will be the isothermal expansion of an ideal gas. In the accompanying figure, an arbitrary amount of an ideal gas is held at a fixed temperature in one side of a two-chambered flask. The initial state of this system of the flask at the instant the valve connecting the two chambers is opened is all of the gas confined to the left chamber. In a spontaneous process, the amount of gas becomes equally distributed between the two chambers.

Definitions of entropy

Qualitative assessment of ΔS for example processes

The following general, qualitative rules allow prediction of the sign of ΔS for many kinds of processes:

• Temperature: The entropy of a system (e.g. a fixed amount of a pure substance) increases as T increases.
• Phases: When of an element or compound is in a gaseous state, its entropy is much higher compared with its entropy in a liquid state. A substance has higher entropy in a liquid state than it does in a solid state.
• Gas phase chemical reactions: The entropy increases if the reaction produces a greater total number of gas molecules.
• The entropy of a solid compound often increases upon dissolution (dispersal throughout a solvent, forming a solution). The "often" in this statement tips us off to recognize the need to examine the thermodynamics of this process a little more carefully.

Thus, we can predict that when a substance evaporates, its entropy greatly increases, or that entropy increases when a chemical reaction results in the net increase in chemical amount (mol) of gas phase species.

Calculating entropy change for a phase transition

Example: Calculate the thermodynamic value ΔS° for the melting of ice at 0°C and 1 atm pressure, given that the standard enthalpy change for this process, ΔH°_273.15 = 6.007 kJ mol⁻¹.

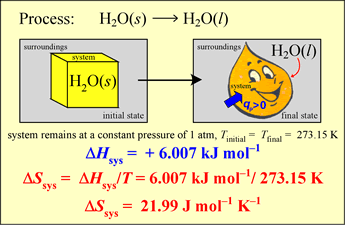
The melting of ice under these conditions is a process occurring at a constant temperature under equilibrium conditions throughout. Therefore we can directly use the classical definition of entropy change in a process,

ΔS°_T =  q_rev / T

which we can also write as ΔS°_T = ΔH°_T / T , since the heat is transferred at constant pressure, so q_rev = q_P = ΔH.

The result is

ΔS°_273.15 =  (6.007 kJ mol⁻¹) / (273.15 K)  =  2.199 × 10⁻² kJ mol⁻¹ K⁻¹  =  21.99 J mol⁻¹ K⁻¹.

Summary of methods for calculation of ΔS

The definition of entropy readily leads to methods to calculate ΔS for several types of processes:

• For phase changes, use ΔS = ΔH / T. (See example above)
• For isothermal expansion of an ideal gas, use ΔS = nR ln(V₂/V₁).
• For chemical reactions and formation of solutions, use S° values from tables as follows: For a generalized reaction, aA + bB + cC + ····   =   xX + yY + zZ + ···· ,
  use the formula
  ΔS°_rxn  =  x S°_X  +  y S°_Y  +  z S°_Z  + ····    − a S°_A  −  b S°_B  −  c S°_C  −  ····

One more method:

For for heating and cooling of a substance, use ΔS = C ln( T_f ,/T_i ), where C is the extensive heat capacity of the system. Note that C is assumed constant over the temperature range and constant pressure or constant volume heat capacity should be specified.

Microstates and macrostates: A statistical view of entropy

Although classical thermodynamics makes no assumptions concerning the ultimate nature of the matter that makes up a system, in order to interpret the Boltzmann statistical mechanical definition of entropy, the ways in which the energy of a system is distributed among its constituent atoms and molecules must be examined. In fact, in order to evaluate the quantity Ω (also often represented as W), the number of so-called microstates must be counted. A microstate is one particular apportionment of the total internal energy of a system among the nanoscale entities of which it is composed, such as our ideal gas example. Because of the dynamic nature of the nanoscale realm - atoms and molecules are in constant motion and engage in collisional processes that redistribute the energy of a system - the microstate of a system is constantly changing. The macrostate of the system, on the other hand, is what we have in mind when we refer to the state of the system, which is specified by the values of macroscopic state variables (P, V, T, n₁, n₂,...). In order for a macrostate to be well-defined, however, the system must be sufficiently large so that the vast number of nanoscale entities it contains ineluctably determine the values of state variables by sheer statistical weight. For an isolated system at equilibrium, these "macro" state variables remain constant with time despite the underlying nanoscale dynamism. Thus, it must be the case that every accessible microstate of such a system is consistent with the total (macroscopic) energy of the system. Such microstates are said to be energetically equivalent, or isoenergetic microscopic states. For a real system with ~10²⁴ particles, there are always a vast number of microstates consistent with or possible for a given observable macrostate.

Microstates, an energy-level view example

Consider a system consisting of four atoms, in which three quanta of energy are distributed. Below right is shown a possible configuration. How many possible configurations are possible, and within each configuration how many permutations are possible?

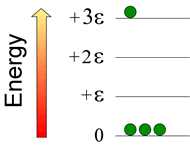
The number of permutations is given by the formula N!/(n₀!n₁!n₂!···n_j! ), where N is the total number of atoms in the system, j is the total number of energy quanta in the system, and n_i is the number of atoms in the ith energy level. Note that i ≤ j, and ∑n_i = N. In this example, the configuration for the N = 4 case (with total energy = +3ε), the number of permutations computes to 4!/{(3!)(0!)(0!)(1!)} = 4·3·2·1/(3·2·1) = 4 (where 0! = 1, by definition). Of course, one could enumerate the permutations in each case by numbering the little green atoms and writing out each distinguishable way of arranging the numbered atoms in a given configuration.

There are two other configurations possible for this case: One has two atoms in the zero-energy level, one atom in the +ε level, and one atom in the +2ε level. There are twelve permutations of this configuration. The last configuration has one atom in the 0 level, and three atoms in the +ε level. For this configuration, there are four permutations. The highest entropy configuration is the second one, since it has the highest number of permutations (12).

Work is another concept that admits a precise definition in physics. Furthermore, the laws of mechanics can be tied in with energy by means of the work-energy theorem. A kick of a soccer ball, or any number of similar examples, illustrates the idea that the kinetic energy of an object can be increased by application of a force. The work-energy theorem, which is a generalization of this idea, can be stated roughly as follows: The change in the energy an object possesses is equal to the magnitude of the force acting on it, multiplied by the distance through which the force acts.

The energy change occurring in a system as a result of work can be positive or negative, from the point of view of the system. Work can be done by a system, or a system can have work done upon it by the surroundings. If work is done by a system, it loses energy to the surroundings. If the system has work done upon it, the energy of the system is increased. For example, when a spark setting off a combustion mixture in a cylinder with a movable piston causes a rapid expansion of the system, and the expansion is mechanically coupled to the motion of a rod in the surroundings, the system of the cylinder does work on the surroundings, and in so doing, loses energy. This of course is a part of how an internal combustion engine converts chemical potential energy into the kinetic energy of a car in motion.

One implication of the work-energy theorem is for units, namely that work can be measured in the same units as energy. Since Newton's second law is force = mass × acceleration, the newton (N), the SI unit for force, is derived as M × L × T  ⁻², and thus 1 N = 1 kg m s⁻². Force times distance has quantities M × L² × T  ⁻², and so the SI unit for energy, the joule (J), is defined as 1 J = 1 kg m² s⁻². At this point, you should verify for yourself that the equation for kinetic energy involves the same combination of the fundamental quantities mass (M), length (or distance, L), and time (T).

Heat and temperature

We use the words heat and temperature quite frequently, and often speak of heat as a form of energy. We all have an intuitive sense of what these things are, but here we want to think about them more scientifically, and give them more formal definitions if we can. This is a necessary prelude to the quantification of the energy corresponding to heat, and thence to measurements to verify the law of conservation of energy. What we find is that the heat energy of a system may be likened to the total kinetic energy (as defined above) of the atoms and molecules that compose it. The temperature of an object or system is actually a measure of the average kinetic energy of the constituent atoms and/or molecules. (N.B. Temperature is not exactly equal to the average molecular kinetic energy, but is directly proportional to it. For further details, see the kinetic molecular theory web page.)

One way to visualize what we mean by heat and temperature, and the distinction between them, is to consider a billiard ball analogy. In some simple contexts, the behavior of billiard balls are an adequate model for a collection of atoms or molecules, such as in a sample of a gas. Just like billiard balls that have been just struck by a rapidly moving cue ball, the molecules of a gas are moving all about, bouncing off each other and the walls of the container holding them. The total kinetic energy of the billiard balls, which is just the sum of the individual kinetic energies of each ball, is analogous to the thermal energy content of a sample of gas molecules. In a "break" at the start of a game of billiards, the initial kinetic energy of the cue ball is distributed among all the balls on the table. Some are moving quite fast, and others not so fast, but the analogy to "heat" or "thermal energy" for the system of billiard balls is just the sum of these kinetic energies. On the other hand, the temperature of the billiard ball system would be proportional to the average kinetic energy of the ensemble of balls.