GENERAL CHEMISTRY TOPICS
Kinetics and equilibrium
Discussion of the dynamic nature of chemical equilibrium: The equilibrium condition as the balance between opposing (forward and reverse) reactions. Further consideration of the connection between the study of reaction rates (chemical kinetics) and equilibrium. Kinetics, equilibrium, and the reaction coordinate diagram (advanced topic).
Chemical equilibrium is the state of constant composition attained when opposing reaction rates become equal. There is an essential relationship between reaction rates and chemical equilibrium, one that we can describe quantitatively. At first thought, the connection may seem obscure - do we not need to be far from equilibrium to properly measure reaction rates? The dynamic nature of chemical equilibrium means that both forward and reverse reactions can be taking place at significant - even high - rates, but since these rates are equal, no change in concentration is observed over time.
Let us once again use the hypothetical example of a simple, reversible reaction, A = B (such as an isomerization) to show the approach to equilibrium from either pure A or pure B. The interconversion of A and B via two opposing reaction rates is shown by two different progress curves (see figure below). In (i), a reaction vessel starts out with 100% A, and it begins to undergo conversion to B. At very early times (leftmost region of the graph, shaded pink), only a negligible amount of B is present, so the observed rate is that corresponding to the forward reaction, A → B. As B begins to accumulate (middle portion of graph, lavender), some of it undergoes the reverse reaction, B → A. The net rate still favors production of B, so that the concentration of B continues to rise and [A] still drops, but more slowly. The conversion from A to B is still faster than the conversion of B to A, and this is indicated in the figure by the relative length of the arrows in the chemical equation. Finally, enough B is present so that the forward and reverse reaction rates are in balance, and the net rate is zero (right side of graph, purple). These equilibrium conditions, once attained, persist indefinitely.
![Progress curves (graph of concentration vs. time) for the reaction A = B for two different starting conditions:
(i) [A] = 1 M, [B] = 0; (ii) [A] = 0, [B] = 1 M](../chemistry/images/progress_equilibrim.gif)
If the starting conditions are 100% B, as in (ii), the kinetics at very early times (leftmost region of the graph) are dominated by the reverse reaction, B → A. Once some A forms, the rate of the forward reaction begins to pick up. The net rate still favors production of A for a short time (middle graph), but its concentration levels off by ~60 s, having attained equilibrium level. Notably, these equilibrium conditions are the same as those in (i) - this assumes both experiments are carried out at the same temperature.
Kinetics, equilibrium, and the reaction coordinate diagram
To further illustrate the relationship between reaction rate and chemical equilibrium, let's consider the reaction coordinate diagram for our simple, reversible reaction.
This diagram, at right, shows a graph (purple line) of chemical potential energy (vertical axis) versus a "reaction coordinate" (horizontal axis), which here represents the progress of a reaction in which one bond must break and a new bond forms. Examples of such reactions are provided by the many isomerization reactions, such as the interconversion of cis-2-butene and trans-2-butene.
Let us first consider the forward reaction, A → B. Reactant molecules (A) in the system with enough energy to reach the energetic peak, the transition state (symbolized by the double dagger, ‡) can continue forward along the reaction coordinate to conversion to product B.
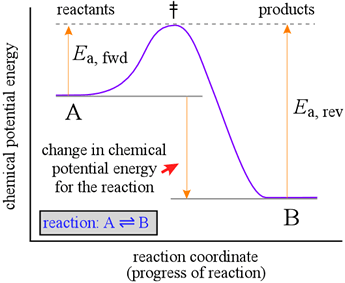
This minimum energy required is the activation energy. For the forward reaction, this is symbolized as Ea, fwd, and is the energetic cost required to advance the bond breaking in a molecule of A to the point where formation of the new bond in B can begin to provide an energetic payback. The increase in potential energy must be provided by the kinetic energy of the molecules in the system, which varies by temperature, according to a Maxwell-Boltzmann distribution. For molecules, the kinetic energy can reside not only in their motion through space, but also in bond stretching, bending, and twisting. Kinetic energy in these forms is constantly being redistributed by collisions between the molecules. We can easily imagine a bond breaking in molecules where an excess of kinetic energy is momentarily transferred into these bond motions. The reverse reaction, B → A, proceeds in a similar manner, but more conversion of kinetic to potential energy at the molecular level is required. Molecules of B in the system with enough energy (the activation energy for the reverse reaction, Ea, rev) to reach the transition state can continue backward along the reaction coordinate to conversion back to A. Since the forward reaction activation energy is less than the reverse reaction activation energy (Ea, fwd < Ea, rev ), the reverse reaction will be slower than the forward reaction when the concentrations of A and B are equal. In order for this reaction to reach equilibrium, the concentration of B will have to increase beyond that of A up to the point where the rates of the forward and reverse reactions become equal. Qualitatively, since Ea, fwd < Ea, rev in this case, Keq > 1.
We can conclude that the net change in chemical potential energy is related to the equilibrium constant
(Keq) for the reaction, whereas the magnitude of the activation energy must be related
to the rate constants for the reaction. Let us specify now that the forward reaction, A → B, and the
reverse reaction, B → A, both follow first-order
rate laws.
Then we can readily derive the relationship between rate constants and the equilibrium constant
for our simple first-order case. The rate laws for the forward and reverse reactions in this case are
forward reaction rate = V0, fwd = k1[A]
reverse reaction rate = V0, rev = k−1[B]
These are just first-order rate laws, with k1 as the forward first-order rate constant, and k−1 as the first-order rate constant for the reverse reaction. At equilibrium, the forward reaction rate is equal to the reverse reaction rate. Setting these expressions equal when equilibrium concentrations are reached, we have
k1[A]eq = k−1[B]eq
which can be rearranged to
k1/k−1 = [B]eq/[A]eq
The right side expression is of course the equilibrium constant for this reaction, so we have shown in this case that
Keq = k1/k−1