BIOCHEMISTRY TOPICS

Heat and heat capacity

What is heat? Heat capacity. Extensive and intensive variables. Specific heat capacity and example. Energy change associated with a process: Phase change example.

---

Of the observable forms of energy associated with chemical change, the evolution of heat perhaps comes most readily to mind. The combustion reactions that warm our homes as well as our bodies illustrate this linkage between chemical change and thermal effects. The production of heat is often taken as evidence that a chemical reaction is occurring, although physical processes can also generate heat. Here we inquire more deeply about the nature of heat as a form of energy, and learn more about how it is measured, transferred, and transduced from other forms of energy. These considerations will serve as a foundation for the study of what is called chemical thermodynamics.

What is heat?

Heat is the exchange of "thermal” energy due to a temperature difference. Consider an isolated system made up of two subsystems initially at two different temperatures.

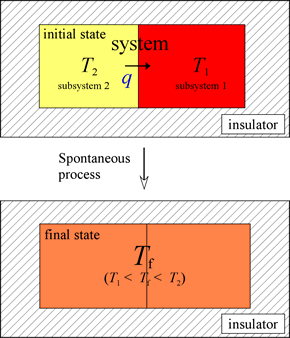
There is a transfer of energy from the higher temperature subsystem 2 to the lower temperature subsystem 1. The amount of energy, which is measurable, is denoted as q. This process, the fundamental features of which we all have experienced, occurs spontaneously. The opposing process, the spontaneous transfer of energy exclusively between two subsystems initially at the same temperature, leading to a difference in temperature, never occurs. This is true even though such a process would not violate the first law of thermodynamics. The prediction of spontaneity relies on the application of the second law of thermodynamics. The distinguishing feature is that the spontaneous process results in an increase of entropy of the system, while in the reverse case, entropy would decrease. A temperature differential can only be generated by the input of energy from the surroundings (e.g. from a flame or burner), in which case the system is no longer an isolated one.

The second law of thermodynamics and entropy provide the means by which the observed, spontaneous direction of a process can be predicted. However, in order to develop these ideas, a theoretical and experimental foundation of heat and temperature is a prerequisite. The main idea here is that the colloquially understood term heat can be defined scientifically as that form of energy that is observable as a result of a difference ΔT in temperature between two systems in thermal contact. As we have recounted, the result of this situation is an exchange of "heat" energy between them until ΔT = 0. As long as the idea of temperature makes physical sense and is measurable, then the quantity ΔT can be used in a relationship with the amount of energy transferred to or from a system.

Let us ask now how to apply the first law of thermodynamics to this example. Since the system is isolated,

ΔU_sys  =  0

and furthermore, there is no heat energy exchanged with the surroundings, nor is any work done on or by the system. This yields the following relations:

ΔU  =  q_sys  +  w_sys  = 0    (since the system is isolated)

q_sys =  0   and  w_sys  =  0    (since the system is isolated)

q_sys =  q₁  +  q₂  =  0

q₁ =  − q₂   (q₁ > 0;  q₂ < 0)

We can apply these basic concepts to the measurement of the energy produced or consumed in the form of heat q for various process's, such as phase changes, formation of solutions, and chemical reactions. The measurement of the energy produced or consumed in processes is termed calorimetry.

Heat capacity

Before we can introduce the techniques of calorimetry, we need to consider the fact that the same amount of energy will produce different values for ΔT when transferred to different substances in the form of heat, q. For example, 1 cal (calorie) of energy was originally defined as the amount of energy required to raise the temperature of 1 g of water by 1 °C. This same amount of energy will raise the temperature of 1 g of a metal by a significantly greater amount: 1 cal raises the temperature of lead by nearly 33 °C! It seems as though substances differ in their ability to accommodate or partition internal thermal energy. This leads us to define the quantity heat capacity.

Total heat capacity is an extensive variable with units J °C⁻¹ (or J K⁻¹). An extensive variable or quantity is one that depends on the amount of substance under consideration. For example, mass and volume are both extensive quantities. An intensive quantity is one that does not depend on the amount of substance, but is the same regardless of how much stuff we look at. Density, which is the ratio of two extensive quantities, mass and volume, is a good example of an intensive quantity. The density of a pure substance, such as iron or water, is the same whether we examine a large or small sample of that substance.

It is useful to define the intensive quantities specific heat capacity (units J g⁻¹ °C⁻¹) or molar heat capacity (units J mol⁻¹ °C⁻¹). These definitions are shown in the figure (right).

The definition of specific heat capacity (sometimes referred to simply as specific heat) entails a very important relation for calorimetry:

This equation states that the energy gained or lost by a system (here, let us think of the system as a sample of pure substance of mass m that remains a single homogeneous phase) as heat is given by the mass times specific heat capacity times the change in temperature ΔT that occurs.

Heat capacity example

As an application of heat capacity and as a preliminary exercise to our treatment of calorimetry, let us consider the general problem of finding a final temperature given the masses, initial temperatures, and specific heat capacities for subsystems 1 and 2 in our thermal energy transfer example above.

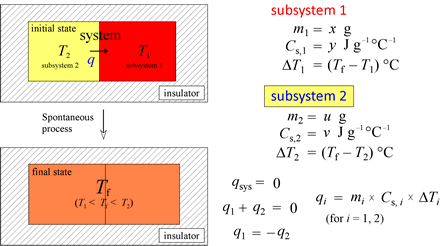
If we use the relations shown at left, we can readily solve for one of the seven variables (m₁, m₂, C_s,1, C_s,2, T₁, T₂, T_f) given the values of the other six.

Example: A 150-g chunk of lead (Pb) heated to 100.0 °C is placed in 50.0 g of water at an initial temperature of 22.0 °C. Given specific heat capacities of lead and water at 0.128 and 4.184 J g⁻¹ °C⁻¹, respectively, and assuming no heat is lost to the surroundings, calculate the final temperature of the lead plus water.

Energy change associated with a process: Phase change example

An energy transfer process can occur with heat q ≠ 0 but with ΔT = 0! In other words, there can be thermal energy exchange without a temperature change. Let us analyze the energetics of a simple phase change example. Our system is an ice cube of mass 18 g at exactly 0 °C. Let us assume that the surroundings are kept slightly warmer than the system, so that spontaneous energy transfer occurs.

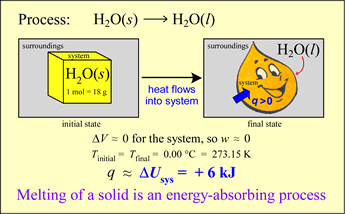
The system will increase in energy as a result since q > 0 and (for reasons that will be evident shortly) the work done on or by the system is negligible. Thus

         ΔU ≈ q < 0 

What happens under these circumstances? The ice melts, gradually it is all converted to liquid water. At the same time, it is observed that the temperature of the system remains constant as long as some of the ice remains. Where does the energy q go if ΔT = 0?

The answer is that there is an energy requirement for the phase change, an input to the system equivalent to the so-called molar heat of fusion. The water molecules in ice are all in hydrogen bond interactions with each other, a particularly strong type of intermolecular attractive force, and the fully-hydrogen bonded water molecules of ice are thereby locked into an ordered lattice that gives the ice cube the shape and solidity characteristic of the solid phase. Some of these hydrogen bond interactions must be broken so that the water molecules can acquire the freedom of motion characteristic of the liquid phase. Virtually all the energy the ice cube system acquires from the surroundings must go into giving the water molecules sufficient kinetic energy to break and loosen enough of the hydrogen bonds to accomplish the complete phase transition. Once all of the ice is converted to water, the further input of energy q from the surroundings would begin to raise the temperature of the liquid water.

Related topics pages:

• thermodynamics introduction
• enthalpy
• second law of thermodynamics
• entropy