BIOCHEMISTRY TOPICS
Chemical thermodynamics: Introduction
Terminology of classical thermodynamics. State variables and the state of a system. Paths and processes. Equation of state: The example of an ideal gas Total internal energy of a system. The first law of thermodynamics
Basic concepts and terminology
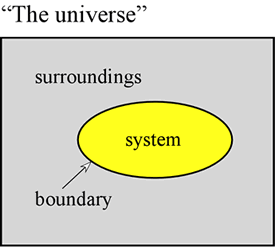
Thermodynamics is a classic scientific discipline of singular logic and rigor, the results of which are of great general applicability. Chemical thermodynamics deals more specifically with phenomena such as phase transitions, reactions, and changes in noncovalent structures. The approach of thermodynamics is to make a distinction at the outset between the part of the universe that is to be studied, which is denoted the system, and everything else. This "everything else" in the in the universe is designated as the surroundings. The system is separated from the surroundings by a boundary, the properties of which are further specified. The boundary may be imaginary or it may correspond to a physical barrier.
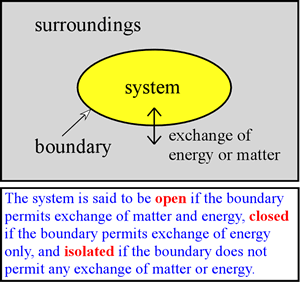
We can envision different types of boundaries and permitted exchanges between the system and surroundings. One of particular interest to us is a closed system in which no matter is exchanged. We further specify that it is possible for the system to exchange energy with the surroundings, so that the system is closed, but not insulated. Therefore it is possible for heat to be exchanged. In addition, the system may do work on the surroundings or vice-versa. In the former case, the system gives up energy to do the work on the system, while in the latter case, the system acquires energy by virtue of the surroundings doing work on it. In any case, the energy gained or lost by the system must be exactly balanced by the loss or gain of energy of the surroundings. This is simply a consequence of the law of conservation of energy (also often referred to as the first law of thermodynamics), which we discuss more formally below.
As an example of a system relevant to chemistry, we may be interested in the system of a gas phase reaction within an enclosed volume. Here, the system is closed but not necessarily isolated. A truly isolated system would require a boundary that does not conduct heat - a perfect insulator - and no such material exists. However, there are reasonably good insulators, such as the walls of a thermos bottle, and over a relatively short period of time only a very small amount of heat is transferred to or from such an insulated system. A chemical reaction taking place in a solution contained in a beaker on a laboratory bench can also be treated as a closed system, at least if no gases are produced or consumed in the reaction, and if our critical observations are made on a time scale over which evaporation of solvent is insignificant.
In developing thermodynamic principles, much use is made of isolated and closed systems, and the emphasis is placed upon equilibrium conditions. Ultimately, however, in a thermodynamic analysis of biological systems, we are forced to consider that living organisms constitute open systems that exchange matter and energy with their surroundings. Furthermore and remarkably, as systems living organisms are not at equilibrium, but instead are autonomous systems that generate and control flux of matter and energy through them to maintain a nonequilibrium steady state.
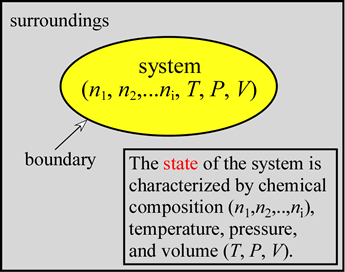
The idea of the state of the system is fundamental. The state is determined by specifying all relevant state variables, namely the chemical composition (moles of substances 1, 2,..., i), as well as the temperature (on an absolute scale, i.e. in kelvins, K), pressure, and volume. Defining the state of the system will also determine the total internal energy, a thermodynamically important quantity that we'll examine more carefully below. If we have in mind either of the chemical reaction examples, the reactants at a certain temperature, pressure, and volume will correspond to an initial state of the system. In the final state - at the end of the reaction - products will be present at some final T, P, and V. It may be most convenient if these values are the same as the initial T, P, and V and if the system under consideration can be treated as closed. This allows us to focus on the energetics of the chemical reaction alone and simplifies the theoretical analysis. Perhaps our single most important goal in studying such systems of chemical reactions is to understand that the process by which they spontaneously approach the state of equilibrium is determined by progress toward a minimum of a thermodynamically defined function of the state of the system called the free energy .
Classical thermodynamics deals with macroscopic systems, those we can readily observe and measure in the laboratory. The state variables temperature (T), pressure (P), and volume (V) are of course quantities subject to measurement, and we employ the mole as a unit of measurement for the amounts of different substances present in the system. Strictly speaking, though, the methods and results of thermodynamics are independent of the molecular and atomic nature of matter. (We could have chosen masses of the chemical components of the system.) These state variables are not all independent. For example, we know that in general, the volume of substances increases with temperature. In fact, there is an equation of state that expresses mathematically the interdependence of the state variables. In the case of an ideal gas, which we discuss further below, an explicit equation of state is the well-known ideal gas law, PV = nRT.
When we study specific systems we are interested in processes, such as chemical reactions, where the system undergoes measurable change. We can define the changes a system may undergo in the formalism of thermodynamics. By change of state, we mean any change from an initial state, specified by an initial set of values of the state variables, to a final state. The final state is, of course, specified by its own set of values of the state variables. Considering the number of state variables, there may be innumerable processes that begin and end with a specified pair of states. The path specifies exactly how the state variables change for a given process starting at an initial state a and ending with a final state b. The path can be thought of mathematically as a curve in n-dimensional space. Although we can imagine an unlimited number of such curves, any equation of state will constrain the possible paths. In practice, we consider a limited number of processes of special interest or usefulness.
 |
 |
In considering examples of processes, convenient use is made of the concept of an ideal gas. The behavior of real gases approximates that of an ideal gas in the limit of low pressure, and temperatures considerably above the boiling point. An example of a process involving an ideal gas is an isothermal expansion of n moles of a pure ideal gas at a constant temperature T, from initial pressure Pi and volume Vi, to a final pressure Pf and volume Vf.
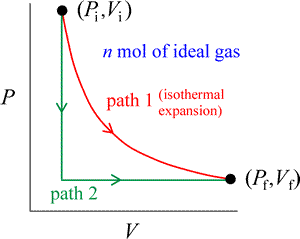
This process is represented by path 1 (in red) in the figure at right, a two-dimensional plot of pressure vs. volume. The ideal gas equation of state tells us not only that PiVi = PfVf, but also that PV is constant for the whole process. An expansion means that ΔV = Vf – Vi > 0. Instead of the isothermal path, we could choose to carry out the same change of state by a different path (path 2, in green). The gas could be cooled at constant volume until the pressure Pf is reached. Following this, the gas is expanded to Vf at constant pressure, which requires the temperature of the gas to rise back to its initial value.
State functions. The example of total internal energy, U.
While we have already mentioned energy and its forms, heat and work, we have yet to define energy as a conserved quantity and a state function. If we account for energy inputs and outputs for a given system, we can study the energetics of various processes. In particular, we can investigate what drives processes that seem to occur of their own accord - that is, they occur spontaneously - versus what is simply possible when there is no energy input to the system.
In principle we can account for all the energy in a system. Let us define this as the total internal energy of the system, and denote it as U. (Often the symbol E is used, but we will use U for energy in this context.) Usually we will refer to the total internal energy of a system simply as its energy.
An important property of energy is that it is a state function. A state function is a function whose value is dependent only on the state of a system, and the changes in a state function when a system changes from one state to another are path-independent. This means that no matter what path (sequence of changes in chemical composition and other state variables) a system takes in going from state 1 to state 2, the change in value of the state function is the same. Another way of expressing this is to say that the value of a state function is determined solely by its current state, and not by its "history" (exactly how it got to that state).
Conservation of energy: The first law of thermodynamics
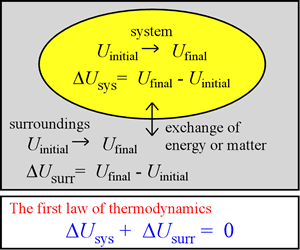
In the foregoing, several examples were presented of systems we can consider from our chemical thermodynamic perspective. What types of energy do such systems possess? What can be said regarding processes occurring in these systems that involve changes in their internal energy? The first law of thermodynamics, which we put on a firm basis in this section, is an important statement that applies to any process.
For any process, the change in internal energy U(n, T, P,V) is in general expressible as the final value of U minus its value before the process has occurred. This energy change is written as ΔU. Because the actual value of U is quite large, it is only practical to measure ΔU. There are two quantities, heat and work (described further below) that - when measured for a process involving no matter exchange - determine ΔU for the process. The results of such measurements have demonstrated that any gain or loss of energy ΔUsys is exactly compensated for by loss or gain of energy by the surroundings, ΔUsurr. In other words, energy is neither created nor destroyed in any process, and is thus always conserved. This is a clear statement of the first law of thermodynamics.
The equation ΔUtotal = ΔUsys + ΔUsurr = 0 is of course the mathematical formulation of this statement. The first law of thermodynamics has been established by many careful measurements of the heat and work associated with various processes. Let us consider the nature of heat and work.
Heat can be described as a form of energy that is transferred between system and surroundings as a result of a temperature difference between them. The conventional symbol for this form of energy is q.
Work (in general symbolized as w) can be divided into different types. Most commonly, we consider mechanical and electrical work. The definition of mechanical work from physics - in its simplest form - is that work is a quantity corresponding to a constant force F acting through a distance d. We will consider mechanical work in the form of pressure-volume work (P-V work). If a gas in a closed system with a movable boundary - such as a balloon or a piston within a cylinder - expands against an external pressure Pext, work has been performed by the system, and the amount of work is given by the relation w = –Pext(ΔV). The system is said to have done work on the surroundings, and in this case, the sign of w is negative, since this will correspond to a loss of energy from the system. You should verify that both the products P·V and F·d give rise to units of energy.
We will see from examples of processes that both the amount of heat transferred q and the work w done will depend on the particular path a process follows in taking the system from an initial state to a final state. Imagine a closed system in which a process occurs, accompanied by a change in volume of the system. In this case, the system may do work on the surroundings or vice-versa. In the former case, the system gives up energy to do the work on the system, while in the latter case, the system acquires energy by virtue of the surroundings doing work on it.
Energy changes and examples of energy conservation
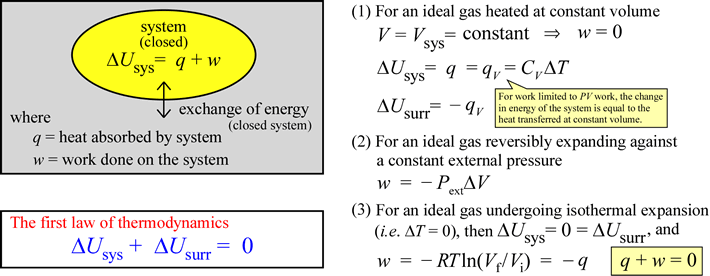
The equation ΔUsys = q + w can be taken as a statement of the first law of thermodynamics under the conditions we have specified, since under these conditions we have accounted for all energy inputs and outputs from the point of view of the system, with the constraint that total energy of the universe remains constant satisfied. In some discussions of the first law, one will see the equation written as ΔUsys = q – w, in which work done by the system on the surroundings is given a positive sign. This is the first law from an engineer's point of view, since engines are systems capable of performing useful work (on the surroundings) given an energy input. A heat engine - the classic example being a steam engine - can take energy in the form of heat and produce mechanical work, such as the rotation of a driveshaft. We will use the convention that work done by the system on the surroundings is negative in sign, since this keeps our attention focused on the energy balance sheet of the system of interest. Heat transferred to or work done on the system (q or w positive) increases its internal energy. If the system gives up heat to the surroundings (q negative), or performs work on the surroundings (w negative), its internal energy must correspondingly decrease.
Related topics pages: