BIOCHEMISTRY TOPICS
Enthalpy
Enthalpy and thermochemistry. Enthalpy change for a process is the quantity of heat transfered at constant pressure. Enthalpy is a state function. Enthalpy change for a phase transition. Thermochemical equations and enthalpy changes for chemical reactions. Standard enthalpies of formation and their use.
Enthalpy and thermochemistry
For a process occurring at constant pressure, the heat exchange to or from a system, designated qP, is of special significance since it represents the change in the value of a state function. This state function is called enthalpy, and it is given the symbol H, and enthalpy changes are designated as ΔH. Thus,
ΔH = qP
and to keep track of enthalpy changes for various processes, such as chemical reactions, the exchange of heat at constant pressure is measured. If a process does not involve a phase transition (or change in allotropic form of an element), then the heat exchange will result in a change of temperature of the system
ΔH = qP = CP ΔT
where CP is heat capacity of the system at constant pressure (an extensive quantity). If we consider a pure substance, with molar heat capacity cP, we can write
ΔH = qP = CP ΔT = ncPΔT
The relation of enthalpy H to internal energy U is central to its defintion as a thermodynamic function. Specifically, enthalpy of a system is defined as
H = U + PV
and the enthalpy function so defined is a state function, since each of its components are also state functions. Defining the enthalpy is useful precisely because of the relationship ΔH = qP introduced above. The enthalpy changes for chemical reactions occuring in aqueous solution under atmospheric pressure can generally be conveniently measured. Furthermore, as biochemical processes mostly occur under conditions of constant pressure, the enthalpy function is better suited than internal energy to biochemical applications.

We also see that for processes at constant pressure accompanied by small changes in volume, ΔH and ΔU are approximately equal. Generally speaking, differences between ΔH and ΔU for chemical reactions are not significant unless gases are produced or consumed.
Finally, if work is restricted to pressure-volume work, then for any constant pressure process the work w is given by w = −Pext(ΔV), and since ΔU = q + w,
ΔH = ΔU + PΔV
ΔH = qP − PΔV + PΔV
ΔH = qP
which shows that the change in enthalpy for a process is measurable as the amount of heat lost or gained by system when the process is carried out under conditions of constant pressure.
Enthalpy change for a phase transition
An energy transfer process can occur with heat q ≠ 0 but with ΔT = 0! In other words, there can be thermal energy exchange without a temperature change. Let us analyze the energetics of a simple phase change example. Our system is an ice cube of mass 18 g at exactly 0 °C. Let us assume that the surroundings are slightly warmer, so that spontaneous energy transfer occurs.

Thermochemical equations and enthalpy changes for chemical reactions
Thermochemical equations are the balanced chemical equations for a process or reaction together with one or more quantities representing the accompanying changes in the thermodynamic functions per mole for the reaction as written. Since we are discussing enthalpy, we will write thermochemical equations with their corresponding enthalpy changes (ΔH). For example, for the physical process of ice melting represented above, we would write
H2O(s) → H2O(l) ΔH = +6.007 kJ
When writing thermochemical equations for chemical reactions, the preceding example should remind us that it is crucial to specify the physical state of all reactants and products. For example, under standard conditions
2 CH3OH(g) + 3 O2(g) → 2 CO2(g) + 4 H2O(g) ΔH = − 1352.2 kJ
which is to be compared to
2 CH3OH(l) + 3 O2(g) → 2 CO2(g) + 4 H2O(l) ΔH = − 1453.0 kJ
Standard enthalpy (ΔH°) values are defined as the ΔH values measured for processes or reactions involving substances in their standard states under standard conditions. Standard state for a gas is defined is the pure gas at a pressure of exactly 1 bar (many sources give 1 atm as standard state). For a liquid or solid, standard state is the pure liquid or solid (in its most stable form at a specified temperature) under an ambient pressure of 1 bar. Although not formally part of the definition of standard state, the temperature should also be specified. Usually 25 °C (298 K) is chosen, and in cases for which this is not made explicit, 25 °C will be assumed. For substances in solution, standard state is defined as a concentration of exactly 1 M. For thermodynamic quantities such as ΔH, their values under standard conditions (all relevant substances involved in the process in their standard states) is indicated by the ° symbol.
Enthalpy is a state function: Path independence
Path-independence means that no matter what path (sequence of changes in chemical compost ion and other state variables) a system takes in going from state 1 to state 2, the change in value of the state function is the same. Another way of saying this is that the value of a state function is determined solely by its current state, not by its "history" (exactly how it got to that state). The figure below, which represents enthalpy changes along a vertical axis, illustrates the idea of path independence for the example of the formation of diatomic hydrogen. If we include oxygen in our system, we can imagine the same process occurring in the presence of oxygen. As long as oxygen remains unchanged, the enthalpy change for the reaction converting H atoms to H2 molecules remains the same, – 435 kJ/mol (the downward red arrow in the figure). However, given the presence of oxygen in the system, we can also imagine an alternate path - path 2 - connecting the two states (the three consecutive blue arrows - steps a, b,and c). The sum of the enthalpies for the three steps is – 435 kJ/mol, thus ΔH is the same for two different paths connecting the same two states. This is actually just another way of saying enthalpy is a state function.
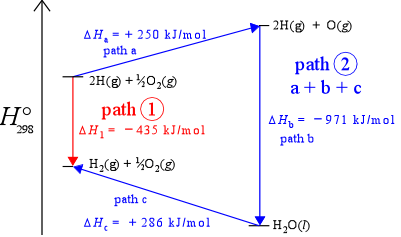
Enthalpy is a state function: Thermodynamic cycles
Since enthalpy is a state function, we can rely on the fact that there is no net change in its value for a cyclic process. In a cyclic process, the path followed is such that the initial and final states are the same. Thus, ΔH = 0 for a thermodynamic cycle. As an example of how this can be applied, consider the two reactions that produce hydrogen and oxygen gas shown in part (a) of the figure below, which show examples of enthalpy diagrams. Given the values of ΔH° as shown, the ΔH° of a third reaction can be computed, since we can construct a thermodynamic cycle from the three reactions. The cycle begins and ends with 2 mol water and 1 mol oxygen at standard state, as shown in part (b) of the figure. That the value of ΔH° for the reaction in which hydrogen peroxide is converted into water and oxygen can be directly calculated is illustrated in the enthalpy diagram.
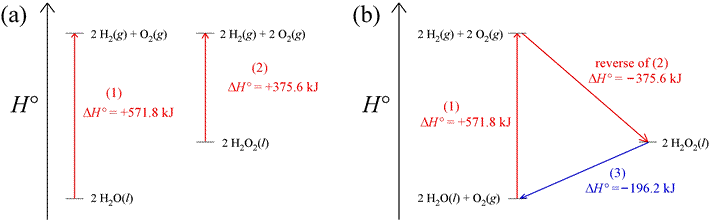
Standard enthalpies of formation and their use
Thermodynamic quantities known as standard enthalpies of formation have been measured for a great many compounds and can be used in a systematic method to calculate the enthalpy change for any reaction involving these compounds as reactants or products. The standard enthalpy of formation (ΔHf°) of a substance is defined by the thermochemical equation for the formation of 1 mole of that substance from its elements in their most stable states under standard conditions. (As stated above in connection with the definition of standard state, the additional specification of temperature is usually for 25 °C (298 K)).
For example, the (thermochemical) equation for the standard enthalpy of formation of glucose would be
6 C(s, graphite) + 6 H2(g) + 3 O2(g) → C6H12O6(s) (ΔH = ΔHf° = − 1273.3 kJ/mol)
Note that the most stable allotrope of an element (in this case, the graphite form of carbon) is specified for the definition of standard enthalpy of formation.
Tabulated values for ΔHf° for many different substances are readily available, usually found in an appendix of a general chemistry textbook. The standard enthalpy of formation of the most stable form of an element at the specified temperature is zero by definition.
The procedure to calculate the standard enthalpy change (ΔH°rxn) for a generalized chemical reaction,
aA + bB + cC + ···· → xX + yY + zZ + ····
is to combine the ΔH°f values for the products and reactants according to the formula
ΔH°rxn = x ΔH°f, X + y ΔH°f, Y + z ΔH°f, Z + ···· − a ΔH°f, A − b ΔH°f, B − c ΔH°f, C − ····
This formula, based on the principle of Hess's law, is sometimes referred to as Hess's law equation. It should be noted that the stoichiometric coefficient could be interpreted as introducing the unit mol to each of the ΔH°f values, given in kJ mol−1, so that the ΔH°rxn we compute is an extensive quantity. Alternatively, we can interpret the value intensively (keeping the stoichiometric coefficients unitless) as the amount of heat released or absorbed per mol of the reaction as written.
Example: Calculate the thermodynamic value ΔH° for the following reaction at 298.15 K (25.00 °C):
N2(g) + 3 H2(g) → 2 NH3(g)
Use the values for standard enthalpies of formation given in thermodynamic tables (these are usually found in an appendix of a general chemistry textbook).
Solution: We need the ΔH°f value for NH3(g). Note that we don't need the value for molecular nitrogen gas or diatomic hydrogen gas, since these are the most stable forms of these substances at 25°C, and their ΔH°f values are zero by definition. To get the standard enthalpy change for the reaction, multiply the ΔH°f values by their stoichiometric coefficients in the chemical equation above (along with the unit "mol"), but using a minus sign for reactants, and then add up all the terms, as shown below:
ΔH° = 2 mol · [ ΔH°f {NH3(g)}] = 2 mol · [ − 46.11 kJ mol−1 ] = − 92.22 kJ
The resulting thermochemical equation is then
N2(g) + 3 H2(g) → 2 NH3(g) ΔH° = − 92.22 kJ
Related topics pages: