BIOCHEMISTRY TOPICS

Problems in redox biochemistry

Biological redox reactions. Using the Nernst equation.

---

Problem 34-3: Biological redox reactions

The following reaction occurs in a muscle working under anaerobic conditions:

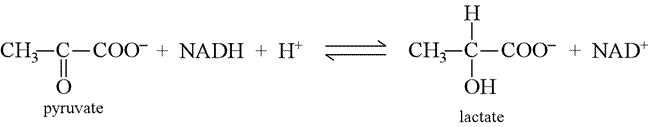
By using oxidation numbers as an "electron bookkeeping" device, show explicitly the reduction of pyruvate to lactate. Write half-reactions using the correct number of protons and electrons for the reduction of pyruvate to lactate, and for the reduction of NAD⁺ to NADH. The change in oxidation number when pyruvate is converted to lactate can be used to find the right number of electrons transferred in the half-reaction.

Solution: In the reduction of pyruvate to lactate, the oxidation number of the central carbon atom changes from +2 to 0*, so the number of electrons transferred in its balanced half-reaction is 2. Another way to look at this is to count the change in number of bonds from carbon to oxygen. Only the central carbon atom is changing in this reaction. Since there are two bonds to oxygen from this carbon atom in pyruvate, and one in lactate, an electron pair has been gained by this carbon atom (electron pairs in C—O bonds are counted as "owned" by (or assigned to) the more electronegativity oxygen atom, while those in C—H bonds belong to the slightly more electronegative carbon as a result of (formally) a two-electron reduction. Furthermore, the structural formulas show that pyruvate gains two hydrogen atoms in being converted to lactate, and we note that in the organic chemistry terms of functional groups, the ketone of pyruvate is reduced to a secondary alcohol in lactate. This reduction is analogous to that of formaldehyde to methanol, as shown in the biological oxidation-reduction reactions topics page.

pyruvate  +  2H⁺  +  2e^–  →  lactate

This half-reaction, added to the reverse of the reduction half-reaction for NAD⁺ must yield the net reaction shown above. The half reaction for NAD⁺ reduction is therefore

NAD⁺  +  H⁺  +  2e^–  =  NADH

*Details on oxidation number assignments. In explicitly assigning oxidation number, we always compare the number of valence electrons of an atom with the number of electrons in bonds to less electronegative (EN) atoms. Thus, for formaldehyde, the oxidation number of carbon is zero because (a) carbon has four valence electrons, (b) the four electrons in the two bonds between C and O are assigned to oxygen, but (c) carbon gets the four electrons in the two other bonds to the slightly less EN hydrogen atoms. Taking the difference between valence electrons and "assigned" electrons leads to an oxidation number for this carbon of 4 − 4 = 0. But what about the central carbon in pyruvate? Even though there is very little difference in EN between C and H, carbon-carbon bonds have to be treated differently by convention. Since the same atoms have the same EN, then the two electrons in each carbon-carbon bond have to be split between the two atoms. Carrying through this process for the central C atom in pyruvate, it is assigned two electrons - one from each of the two carbon-carbon bonds, and nothing from the double bond to oxygen. Thus the actual oxidation number for this middle carbon must be 4 − 2 = 2. The oxidation number for other carbon atoms in the molecule: carboxylate carbon (C1) = 4 − 1 = 3; methyl carbon (C3) = 4 − {1 + 3(2)} =  −3. If you add up all oxidation number for all atoms - using +1 for every H and −2 for every O, you will obtain −1, the net charge on the molecule. Lactate can be treated similarly. The oxidation numbers of C1 and C3 will be same, so the only change involves C2. The oxidation number of this carbon is zero because (a) carbon has four valence electrons, (b) the two electrons in the two bonds between C2 and O are assigned to oxygen; (c) C2 gets the two electrons - one from each of the two carbon-carbon bonds, and (d) in the two other bonds to the slightly less EN hydrogen atoms. Taking the difference between valence electrons and "assigned" electrons leads to an oxidation number for this carbon of 4 − (2 + 2) = 0.

By now it may seem simpler to use the shortcut of counting bonds to oxygen, as suggested above, where each additional bond to oxygen adds +2 to the oxidation number, and a reduction in bonds to oxygen reduces the oxidation number by −2 for each bond to O lost. This works just fine for compounds containing only C, H, O.

In the above relation, γ is the magnetogyric ratio, a constant characteristic of the nucleus being observed in the magnetic field. The equation expresses the condition for a resonant frequency (of electromagnetic radiation) ν_o, which lies in the radio frequency part of the spectrum.

Redox reactions and bioenergetics

Problem 36-1: Biological redox reactions

Lactate dehydrogenase is an enzyme that catalyzes the reversible reaction shown below, which occurs in a muscle working under anaerobic conditions:

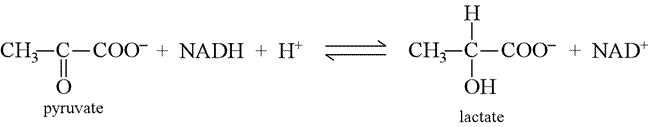
Consulting a table of biochemical standard reduction potentials (e.g. Lehninger 7e, p. 521), write the two half-reactions that comprise this reaction and calculate its equilibrium constant at 37.00 °C using E°′ =  – 0.19 V for the pyruvate reduction half-reaction.

Solution: The half-reactions were obtained in Problem 34-3 (see above). We can show that these two half-reactions can be combined to yield the chemical equation (above) provided.

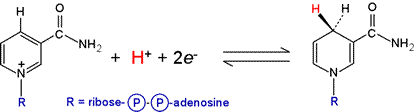
When the number of electrons in each half-reaction are the same, then the reactions can be combined to form the equation for a complete redox as follows:

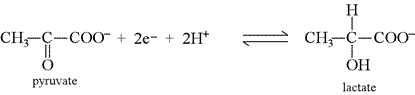
One of the reactions is reversed, and the two equations are added together. The electrons cancel out, and any other species that appear on both sides of the reaction should be appropriately cancelled. In this example, the top reaction is reversed and the two electrons and one proton cancel.

We next calculate ΔE°′ for the reaction, the difference between the two E°′ values. The value we subtract corresponds to the half-reaction we reversed:

ΔE°′  =  – 0.19 V  –  ( – 0.32 )V  =  + 0.13 V

From this we calculate the equilibrium constant at 37°C (310 K) using the equation

K_eq = 10^{nFΔE°′ / 2.3026RT} .

Plugging in n = 2, F = 9.649 × 10⁴ C mol^–1, R = 8.3145 V·C mol^–1K^–1, T = 310 K, and ΔE°′  =  0.13 V, we obtain K = 1.7 × 10⁴.

Problem 36-2: Using the Nernst equation

For the reaction catalyzed by lactate dehydrogenase treated in Problem 36-1 (above), calculate ΔE°′ and ΔG°′ for the reaction when pH = 7.00 and the concentration ratios for both [lactate]/[pyruvate] and [NAD⁺]/[NADH] are both 1000.

Solution: We obtained the result ΔE°′  =   + 0.130 V for this two-electron redox reaction from Problem 36-1 (above). Setting up the Nernst equation fora complete redox reaction under arbitrary conditions

ΔE′ =   ΔE°′   −  {(ln 10)RT/nF}log Q

We will assume that T = 25.00 °C so that the factor (ln 10)RT/F becomes 0.05916 V. Since n = 2 , we can write more specifically for this reaction

ΔE′ =  + 0.130 V  −  (0.05916 V / 2) log { [lactate][NAD⁺] / [pyruvate][NADH]([H⁺]/1 × 10⁻⁷)}

Since pH = 7.00, the activity of H⁺ is 1, and the term drops out of the reaction quotient expression.

ΔE′ =  + 0.130 V  −  (0.05916 V / 2) log { [lactate][NAD⁺] / [pyruvate][NADH]}

Substituting in the given concentration ratios,

ΔE′ =  + 0.130 V  −  (0.05916 V / 2) log {10³ · 10³} = + 0.130 V  −  (0.05916 V / 2) · 6

ΔE′ =  + 0.13 V  −  (0.05916 V / 2) log {10³ · 10³} = + 0.130 V  −  0.1775 V  =  −  0.048 V

To calculate ΔG′, use the relation

ΔG′  =  −nF ΔE′  =  −2(9.649 × 10⁴ J V ⁻¹)( − 0.048 V)  =  9.2₆ kJ

Report 9.3 kJ as the result. The oxidation of lactate to pyruvate is spontaneous under these conditions.

Related topics pages:

• biological redox reactions
• bioenergetics
• electron transport chain
• free energy