BIOCHEMISTRY TOPICS

Models for allosteric behavior in proteins

Monod-Wyman-Changeux (MWC) model.

---

The MWC or "concerted" model for cooperativity and allosteric regulation

A model postulating a concerted change of one fully symmetric quaternary structure into another can largely account for the distinctive properties of hemoglobin. This elegant model, which we'll call the MWC model, accounts for homotropic positive cooperativity, as well as heterotropic allosteric effects. The MWC model is named after Jacques Monod, Jeffries Wyman, and Pierre Changeux, who formulated their model for allostery in 1965. Jacques Monod was one of the great pioneers of molecular biology.

The concept of two distinct symmetric states is the central postulate of the MWC model. For hemoglobin, have seen the structural evidence for at least two distinct quaternary structures, corresponding to deoxy-Hb and oxy-Hb, and these two structures serve as prototypes for of what we could conveniently call T and R states, two fully-symmetric quaternary structures, with distinct affinities for ligand (or substrate). Below, the use of equilibrium concepts to arrive at an equation reproducing a positively-cooperative ligand binding curve is discussed.

The figure below illustrates the MWC model for a hypothetical tetrameric ligand binding protein, with the ligand denoted as A. The subunits of the tetramer are represented as squares or circles, which represent the only two states the subunits can adopt, T (low affinity for A - squares) and R (high affinity, circles). Each protein molecule, whether T or R, can bind 0, 1, 2, 3, or 4 ligands, giving rise to all the equilibria shown.

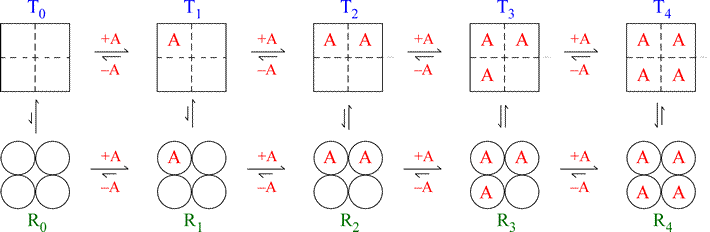
Note that the model is fully symmetric: there are no intermediate states (mixing of squares and circles). The T quaternary state is made up of four subunits (shown as squares) all with the low affinity tertiary structure (we can label each square within the group of four as “t”) with each ligand binding site having a relatively larger K_d value. The R quaternary state is made up of four subunits (shown as circles) all with the high affinity tertiary structure (we can label each circle within the group of four as “r”) with each ligand binding site having a relatively smaller K_d value. The length of the arrows representing the binding equilibria along the horizontal direction of the figure qualitatively indicates this difference in affinities: the upper row of T state binding equilibria compared to the lower row of R state equilibria shows that the ligand binds preferentially to sites on the R state molecule. The relative lengths of the arrows remain the same in both rows all the way across. In contrast, the vertical arrows that represent the equilibria between R and T show qualitatively by their changing lengths that as the ligand concentration increases, and the protein becomes increasingly saturated with ligand, the R ⇔ T equilibrium increasingly favors the R state. This model produces a sigmoidal saturation curve (Y vs. [A]).

In this mathematical description, the model makes use of three parameters: n, which is the number of ligand binding sites per molecule (usually the same as the number of subunits); L, which is defined as the equilibrium constant for conversion of the R state to the T state; and c, the ratio of K_d for the R state to K_d for the T state.

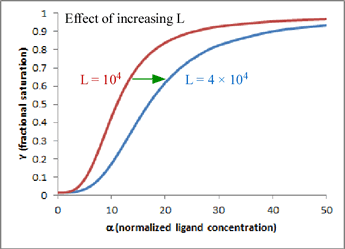
One very satisfying feature of the model is that - in the case of hemoglobin (n = 4) - we can explain homotropic and heterotropic effects in terms of the single parameter L. In particular, positive cooperativity is explained (due to the linkage between binding and conformational equilibria) as a decrease in L as ligand concentration increases. Heterotropic effects, such as BPG binding and the Bohr effect, are explained by the increase in L induced by BPG or H⁺ binding. In the graph shown here, which is a plot of the equation for Y given above, the two curves show the effect of changing L when n = 4 and c is kept fixed at a value of 0.014. Increasing L favors the T state and shifts the sigmoidal curve to the right.

Related topics pages: bioenergetics |

Related topics pages:

• myoglobin
• hemoglobin
• buffers
• carbonic anhydrase
• water