BIOCHEMISTRY TOPICS
Buffers
Definition and properties of a buffer. Buffer pH calculations and the Henderson-Hasselbalch equation.
Buffers
Developing a treatment of pH calculations can be described in terms of four general cases (depending on how you count them): (1) Strong acid / strong base; (2) Weak acid/ weak base; (3) Buffer; and (4) Intermediate forms of polyprotic acids. In the laboratory part of the course also investigates the properties of buffers. Here, examples of calculations used in preparation of buffers, and those used to predict changes in pH of a buffered system occurring upon addition of specified amounts of strong acids or bases are considered. Further practical aspects of buffer preparation and use, including the concept of buffer capacity, are also explored.
The Henderson-Hasselbalch equation
One of the most useful equations in acid-base chemistry is the Henderson-Hasselbalch equation.
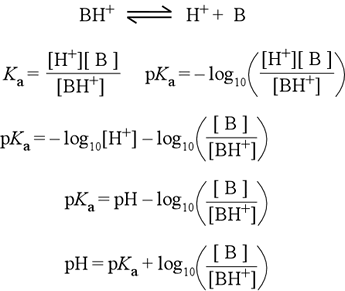
The derivation of the Henderson-Hasselbalch equation for a weak acid of the form BH+ is shown at right. One always starts with the acid dissociation equation, which for BH+ shows the production of the neutral base B and H+. The definition of Ka follows by applying the usual rule for constructing an expression for the equilibrium constant to the acid dissociation equation (line 2). Next, apply the definition of pKa = − log Ka (line 2, 2nd eqn.). The property of the log function log(ab) = log a + log b is used to separate log[H+] from the log([B]/[BH+]) term (line 3), then the definition of pH is applied (line 4). This is essentially the Henderson-Hasselbalch equation, which we write in whatever form is most convenient for the problem at hand. Rearranging this equation (line 5), we have the form commonly presented in textbooks.
The essential buffer calculations
We will denote the total chemical amount of buffer species in a given volume and concentration of a buffer solution as N, measured in moles (mol) or millimoles (mmol). If volume is unspecified, N can be assumed to be the chemical amount of total buffer species in exactly 1 L of buffer of the given concentration (M or mM). By total buffer species we mean the sum of both the acid species form of the buffer and the conjugate base. If one speaks of a buffer at a concentration of say, 50 mM, this means that the sum of the concentration of the acid form and the base form is 50 mM. If we specify a volume and concentration of a buffer solution, let us let a be the chemical amount of the acid species and b represent the chemical amount of the base form. Then we will have
N = a + b
Generally, for the buffer preparation question, having specified a target volume and target concentration for the buffer solution, we then solve the "two equations in two unknowns" problem, a recurrent problem in chemistry and mathematical treatments in many other scientific disciplines. Our two unknowns are a and b. The first equation we need will be the expression for total chemical amount of buffer species N above. Again, this is determined by our choice of concentration and volume. The second equation comes from solving the Henderson-Hasselbalch equation for the ratio r of the chemical amounts b and a of the base and acid forms of buffer, respectively. The value of r is determined by the pKa of the acid form of the buffer pair and target pH we set. Thus, the two equations we set up here are
10pH – pKa = b / a = r
N = a + b
Solving this pair of equations is fundamental to any buffer preparation calculation, as is illustrated in the example problems.
Practical aspects of buffers
- Buffer preparation
- Actual pH vs. calculated pH
- The pKa depends on
- Concentration
- Temperature
- Ionic strength
"My pHcalc ≠ pHmeas"
- pHcalc (and all equilibrium-based calculations) assume ideal solution behavior by using concentrations
- Actual pH is governed by activities (a), rather than concentrations:
- aHA = γHA[HA] where γHA = activity coefficient of HA (For further details, see Ref. 4, Ch.12).
- Activity coefficients tend toward 1 as concentration tends to zero
- Ionic species have much greater coefficients than neutral molecules in general
Buffer capacity
The capacity of a buffer depends on the total (formal) concentration of the buffer species ( [acid] + [conjugate base] ), and for a given total concentration, general buffer capacity will be greatest when [acid] = [conjugate base] - that is, when pH = pKa for that buffer's acidic form.
If one knows in advance that the buffer will need to resist an increase in pH due to the addition of base (or equivalently, consumption of H+), and that protection against acid is not needed, one can prepare a buffer with an initial excess of the acidic species. This would provide an extra measure of buffer capacity in this special situation. A similar idea holds if the buffer must protect against addition of acid and not base: A buffer with an initial excess of the basic species may be called for.
As we see when we study titration curves, the change in pH of a solution that is a mixture of a weak acid and a conjugate base (that is, Aha! A buffer!) that is being titrated with strong base (addition of OH−) is the smallest when the pH reaches the pKa of the weak acid; i.e. when pH = pKa. This can be shown analytically by using the methods of calculus to derive an expression for the derivative of the titration curve. The derivative dpH/dn is the slope of the titration curve, and since this slope will be the smallest (closest to horizontal with pH along the vertical axis) when buffer capacity is greatest, taking the inverse of this expression yields one common definition of buffer capacity, denoted as β:
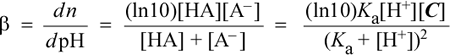
This equation, which is valid for the range of pH values pKa ± 2, shows (as expected) a dependence of buffer capacity on total buffer concentration [C]. The expression reaches a maximum value of ln10[C]/4 when [H+] = Ka. For some applications (such as the situation noted above, where we are concerned with buffering capacity against one or the other of added H+ or OH−, but not both), we can adopt a more practical definition of buffer capacity that takes account of the resistance of a given buffer at a given pH to changes both to added acid and added base. The buffer capacity in the acid direction (BCa ) could be defined as the number of moles of H+ that must be added to one liter of the buffer in order to decrease the pH by 1 unit, and the buffer capacity in the alkaline direction (BCb) as the number of moles of OH− that must be added (per liter) of the buffer in order to increase the pH by 1 unit.
Physiological buffers
As an example of physiologically relevant buffering, consider the carbon dioxide/bicarbonate system diagrammed below:
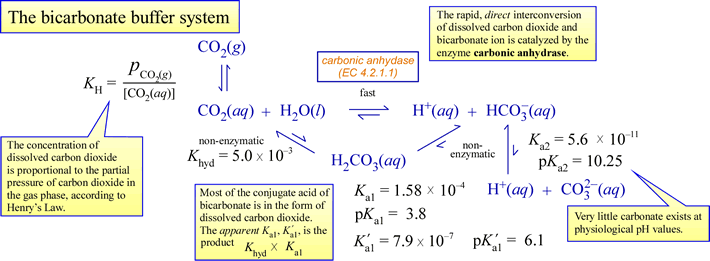
A few important points to tie all the chemistry above to physiology:
- A biological system is open, meaning it exchanges matter and energy with its surroundings. In this scenario, this means (for example) that excess metabolic carbon dioxide is expelled to the surroundings.
- Carbon dioxide is a neutral, nonpolar molecule, and can readily diffuse across membranes. Bicarbonate is a charged species, and does not cross membranes at a significant rate unless facilitated by transmembrane channels.
See the carbonic anhydrase topics page for full discussion.
Related topics pages: