BIOCHEMISTRY TOPICS
Hemoglobin
Tertiary and quaternary structure of hemoglobin (Hb). Allosteric behavior in proteins Cooperative ligand binding.
Summary
While myoglobin, as a monomeric oxygen-binding protein, is presumably limited to hyperbolic saturation, oxygen binds cooperatively to hemoglobin. This gives rise to a sigmoidal form to the oxygen saturation curve for hemoglobin.
A simple, elegant model for the sigmoidal binding curve is the symmetry or Monod-Wyman-Changeux (MWC) model. In this model, hemoglobin adopts two functionally different forms having different affinities for oxygen. This quantitative functional difference is presumably associated with certain structural, or conformational, differences, and interconversion between these could (on general principle) entail changes in secondary, tertiary, and quaternary structure. In a general MWC model, it is stipulated that a lower affinity conformation for a multimeric ligand binding protein (denoted the T state) can undergo a change to a higher affinity state (denoted the R state), and vice-versa. In other words, the R and T forms can rapidly reach an equilibrium. In this case, increasing ligand concentration will drive the equilibrium between R and T toward the R state, a linkage between the ligand binding and R and T interconversion equilibria termed positive cooperativity. We call the effect of ligand concentration on the conformational equilibrium between R and T a homotropic effect. The model can accommodate other effector molecules that bind at sites distinct from the ligand binding site and thereby affect the R and T equilibrium in either direction. These are called heterotropic effects.
For hemoglobin, the molecular details of this switch between R and T are discussed in out text. The heterotropic Bohr effect enhances oxygen transport from the lungs to respiring tissues, as well as carbon dioxide transport in the opposite direction. Another heterotropic effector is the small molecule 2,3-bisphosphoglycerate (BPG), which binds to deoxyhemoglobin, shifting the conformational equilibrium toward the T state. BPG plays a role in high-altitude adaptation. Fetal hemoglobin has a lower affinity for BPG; thus fetal hemoglobin has a higher proportion of R state conformers than adult hemoglobin at any oxygen tension and therefore somewhat greater affinity for oxygen. Hemoglobin is a model for so-called allosteric proteins, proteins that display such cooperative behavior, via homotropic and heterotropic effects. The theoretical models for allosterism are the aforementioned MWC/symmetry model. and the non-symmetric sequential model. Variant hemoglobins are a factor in human pathology. We consider the case of sickle-cell anemia.
Hemoglobin and allosteric behavior in proteins
The study of hemoglobin (Hb) provides some of the most fascinating glimpses of the ways in which protein structure-function relationships explain physiological adaptations. We find it useful to consider a multimeric ligand binding protein such as Hb as a contrast to a monomeric ligand binding protein (in this case myoglobin or "Mb") and to develop the basic models for cooperativity and allosteric regulation. Following this, we will turn our attention to the structural and chemical details behind Hb's ability to be such an effective oxygen transporter.
The properties and physiological roles of proteins made up of more than one subunit can differ in significant ways from monomeric versions of a functionally homologous protein. (By subunit, we mean a separate polypeptide chain). A case in point is the contrast between the tetrameric (consisting of four subunits) hemoglobin and its monomeric counterpart myoglobin in muscle.
Binding of multiple ligands at multiple sites of a protein can lead to very complex behavior. Allostery is the term applied to the phenomenon in which ligands binding at sites distant from one another in a protein structure functionally interact.
The most common result of this functional interaction between subunits is cooperativity. The oligomeric nature of hemoglobin (Hb), for instance, makes possible cooperative effects between subunits, where binding of the ligand to a specific ligand binding site on one subunit affects the affinity of the others for the same ligand. This is termed a homotropic effect. In Hb, the homotropic interactions between oxygen binding sites have the property that binding of one oxygen molecule at one site increases the affinity of the other sites for oxygen - that is, ligand binding in Hb shows positive cooperativity. Allosteric effects can also be heterotropic, involving interactions between different ligands. Heterotropic allosteric effects also occur in hemoglobin. Ligands such as CO2, H+, and 2,3-BPG affect the affinity of the binding sites in Hb for O2.
Non-cooperative & cooperative binding curves
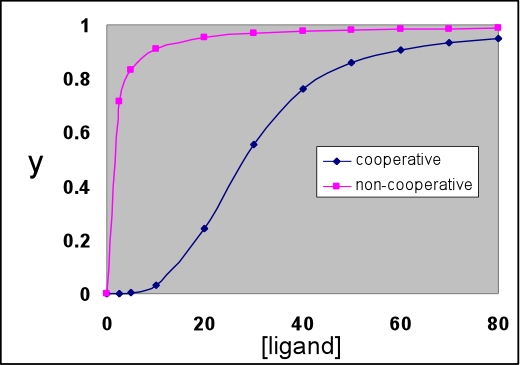
As we have seen for myoglobin, the predicted equation for fraction y of ligand binding sites that are occupied in the case of independent ligand binding sites (e.g. when the sites are on separate molecules) describes a hyperbolic binding curve. That is, when y is plotted as a function of ligand concentration, the value of y at first increases greatly with relatively little ligand added, but as ligand concentration increases the increase in y with the same amount of added ligand drops steadily. Eventually, the asymptotic limit y = 1 is approached. The value of Kd represents the ligand concentration at which half the available sites are occupied, i.e. y = 0.5. The hyperbolic curve described by the following equation represent the non-cooperative binding case.
The graph below shows a cooperative binding curve, and in contrast to the non-cooperative binding curve, it has a sigmoidal shape. This is what is observed for the oxygen binding curve of hemoglobin. Hemoglobin displays positive cooperativity since the binding of the first ligand increases the affinity for the next, and so on. Such sigmoidal curves are characteristic of cooperative transitions between two distinct states that involve the making (or disruption) of numerous weak (non-covalent) interactions.
The non-cooperative binding curve is for Kd = 1. The cooperative curve was calculated according to the symmetry model (see VVP4e, p.192; also known as the concerted or MWC model, with the latter name derived from the names of its originators, Monod, Wyman, and Changeux). This model is described further below.
The MWC or "concerted" model for cooperativity and allosteric regulation
A model postulating a concerted change of one fully symmetric quaternary structure into another can largely account for the distinctive properties of hemoglobin. This elegant model, which we'll call the MWC model, accounts for homotropic positive cooperativity, as well as heterotropic allosteric effects. The MWC model is named after Jacques Monod, Jeffries Wyman, and Pierre Changeux, who formulated their model for allostery in 1965. Jacques Monod was one of the great pioneers of molecular biology.
The concept of two distinct symmetric states is the central postulate of the MWC model. For hemoglobin, have seen the structural evidence for at least two distinct quaternary structures, corresponding to deoxy-Hb and oxy-Hb, and these two structures serve as prototypes for of what we could conveniently call T and R states, two fully-symmetric quaternary structures, with distinct affinities for ligand (or substrate). Below, the use of equilibrium concepts to arrive at an equation reproducing a positively-cooperative ligand binding curve is discussed.
The figure below illustrates the MWC model for a hypothetical tetrameric ligand binding protein, with the ligand denoted as A. The subunits of the tetramer are represented as squares or circles, which represent the only two states the subunits can adopt, T (low affinity for A - squares) and R (high affinity, circles). Each protein molecule, whether T or R, can bind 0, 1, 2, 3, or 4 ligands, giving rise to all the equilibria shown.
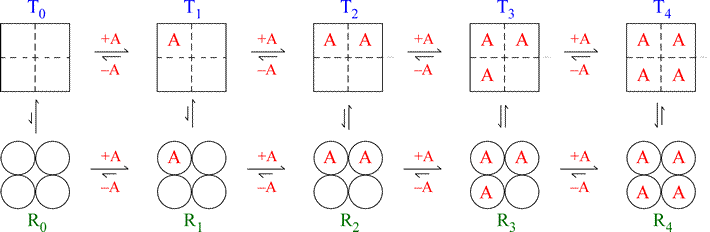
Note that the model is fully symmetric: there are no intermediate states (mixing of squares and circles). The T quaternary state is made up of four subunits (shown as squares) all with the low affinity tertiary structure (we can label each square within the group of four as “t”) with each ligand binding site having a relatively larger Kd value. The R quaternary state is made up of four subunits (shown as circles) all with the high affinity tertiary structure (we can label each circle within the group of four as “r”) with each ligand binding site having a relatively smaller Kd value. The length of the arrows representing the binding equilibria along the horizontal direction of the figure qualitatively indicates this difference in affinities: the upper row of T state binding equilibria compared to the lower row of R state equilibria shows that the ligand binds preferentially to sites on the R state molecule. The relative lengths of the arrows remain the same in both rows all the way across. In contrast, the vertical arrows that represent the equilibria between R and T show qualitatively by their changing lengths that as the ligand concentration increases, and the protein becomes increasingly saturated with ligand, the R ⇔ T equilibrium increasingly favors the R state. This model produces a sigmoidal saturation curve (Y vs. [A]).
In this mathematical description, the model makes use of three parameters: n, which is the number of ligand binding sites per molecule (usually the same as the number of subunits); L, which is defined as the equilibrium constant for conversion of the R state to the T state; and c, the ratio of Kd for the R state to Kd for the T state.
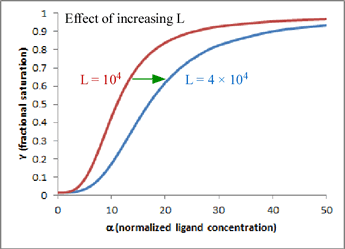
One very satisfying feature of the model is that - in the case of hemoglobin (n = 4) - we can explain homotropic and heterotropic effects in terms of the single parameter L. In particular, positive cooperativity is explained (due to the linkage between binding and conformational equilibria) as a decrease in L as ligand concentration increases. Heterotropic effects, such as BPG binding and the Bohr effect, are explained by the increase in L induced by BPG or H+ binding. In the graph shown here, which is a plot of the equation for Y given above, the two curves show the effect of changing L when n = 4 and c is kept fixed at a value of 0.014. Increasing L favors the T state and shifts the sigmoidal curve to the right.
Related topics pages:
