BIOCHEMISTRY TOPICS
Acid-base chemistry: Part III
Types of pH calculations. Polyprotic acids. Amino acids as polyprotic systems. pH calculations for diprotic species. Principal species analysis of a diprotic system. The phosphate series: An example of a triprotic system.
Here we discuss polyprotic acid-base species, primary examples of which are amino acids. We'll learn the definitions for Ka1, Ka2, Kb1, and Kb2 for a diprotic species, and the relations between these and Kw. We'll then show how to treat pH calculations for each of the three forms of a diprotic system. In this treatment, we largely follow the excellent discussion in Ch. 11 of Harris (Ref.1).
Typical acid-base chemistry questions
What are the concentrations of the possible species in an acid-base system when
- We start with one of the species and make an aqueous solution?
- We have a fixed pH (i.e. a buffered environment)?
In the first case, we want to be able to calculate the pH. In the second case, we are primarily interested in which species – of all those possible - are the principal species.
Polyprotic acids
Acids that have more than one ionizable proton are polyprotic acids. The strong acid sulfuric acid, H2SO4, is a diprotic acid. Its first ionization, represented by the following acid dissociation equation
H2SO4 → H+ + HSO4– Ka ≈ 103
In the second ionization, the amphiprotic hydrogen sulfate acts as an acid
HSO4– → H+ + SO42– Ka = 1.03 × 10−2
Other examples of diprotic acids are the various dicarboxylic acids, such the aliphatic dicarboxylic acids oxalic acid (ethanedioic acid), malonic acid (propanedioic acid), and succinic acid (butanedioic acid). An example of a aromatic dicarboxylic acid that we may have encountered is phthalic acid (benzene-1,2-dicarboxylic acid).
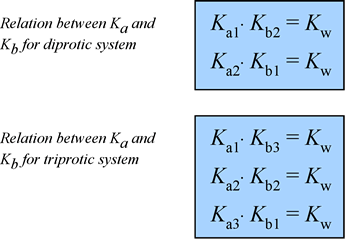
At right is a summary of the relationships among the various Ka and Kb values for diprotic and triprotic systems:
You can derive these relations by combining the chemical equations for the corresponding acid dissociation and base hydrolysis reactions, or by using the expressions for Ka1, Ka2, etc., and Kb1, Kb2, etc. and Kw.
Amino acids as polyprotic systems
Amino acids provide important examples of polyprotics. Most of the biological standard set of 20 amino acids form diprotic systems. A distinct subset have extra ionizable groups and thus are triprotics. Alanine and leucine are examples of aliphatic diprotic amino acids.
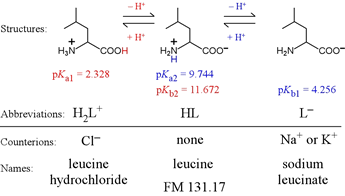
Note the terminology associated with the forms of leucine that we would find as reagents on the shelf, so to speak. The fully protonated form would carry a positive charge and would need to include a counteranion, thus we would find this as (for example) leucine hydrochloride. The intermediate form is neutral, and if we find a reagent named "leucine" this is the form we expect. The fully deprotonated species is negatively charged, and would as a reagent include a countercation, for example, sodium or potassium.
Calculating the pH of a solution of the fully protonated form
For leucine, we can abbreviate the fully protonated form as H2L+. Its acid dissociation equation is therefore
H2L+ → H+ + HL Ka1 = 4.70 × 10−3
We would like to calculate the pH of a 0.0500 M solution of leucine hydrochloride.

If we make the approximation of treating H2L+ as a monoprotic weak acid, following the usual procedure for a weak acid calculation, we substitute [H2L+] = F − x, [H+] = [HL] = x into the expression for Ka1 and solving the resulting quadratic equation, we obtain the results shown at right.
As a check on the quality of our assumption, we can calculate the expected concentration of the fully deprotonated species L− that would result from further dissociation of the intermediate form HL to see if it would significantly alter the equilibrium of the first acid dissociation.
HL → H+ + L− Ka2 = 1.80 × 10−10 = [H+][L−] / [HL]
Rearranging the equation for Ka2 to solve for [L−], and plugging in the values calculated above for [H+] and [HL], we find that
[L−] = Ka2[HL] / [H+] = Ka2 = 1.80 × 10−10 M
Since this value is about eight orders of magnitude less than [HL], the amount of L− formed in the 0.5000 M solution of leucine hydrochloride is miniscule and can be safely neglected, and we see that our approximation is indeed superb.
Calculating the pH of a solution of the fully deprotonated form
Here, we follow a procedure similar to that above, in that we'll treat L− as a monobasic species and perform a weak base calculation.
L− + H2O → HL + OH− Kb1 = 5.55 × 10−5 = [HL][OH−] / [L−]
The pH found is 11.21, and the concentration of H2L+ that would be formed in such a solution can be easily neglected.
Calculating the pH of a solution of the intermediate form
This might appear to be the toughest case. The simplifying assumption that rescues us here is:
If we start with an intermediate species of a polyprotic acid, we will assume that its concentration remains essentially the same.
The pH calculation then becomes quite simple:
pH = ½(pKa1 + pKa2)
This works well as an approximation due to the fact that the amount of intermediate form that is converted to its conjugate acid form is balanced by an approximately equal amount of intermediate form that equilIbtaes eith its conjugate base.
Principal species analysis of a diprotic system
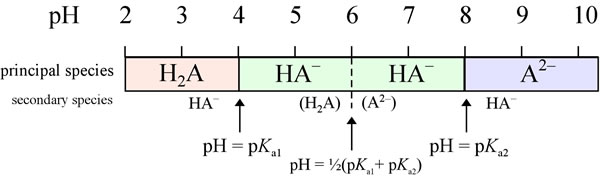
Let us consider a diprotic acid H2A with (pKa1 = 4.00, and pKa2 = 8.00. What will be the principal species as pH varies? Below the first pK value, the fully protonated H2A is the principal species, with the next most abundant species (the "secondary" species) is HA−. The amount of the fully deprotonated form A2− is negligible. As pH increases, the amount of HA− relative to H2A rises, until at pH = pKa1we have [H2A] = [HA−]. Thereafter, continuing increase in pH makes HA− the principal species, and H2A is the secondary species. When pH reaches the midway point between pKa1 and pKa2 (at the dashed line), finally enough A2− is present to make its concentration equal to that of H2A. Both secondary species will be quite low in concentration in this case, since the pK values are well separated. As pH increases further, the amount of H2A is negligible. Before pH rises to equal pKa2, the principal species remains HA−. But when pH = pKa2, [HA−] = [A2−]. At all higher pH values, A2− is the principal species, and HA− is a distant second.
The phosphate series: An example of a triprotic system
Phosphoric acid, H3PO4, is a triprotic acid. The Lewis structures and pKa values of the ionization states of phosphate are illustrated in the figure below.
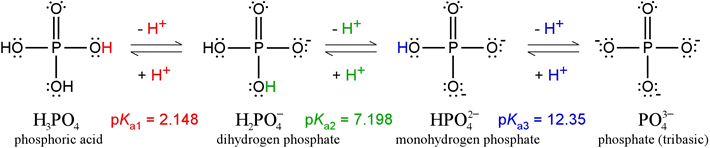
The pKa values shown illustrate the nomenclature used in polyprotic systems: pKa1 corresponds to −log of the first acid dissociation constant, pKa2 to the second, and so on. (Note that some sources will drop the subscripted "a", and speak of K1, K2, etc., where it should be clear from the context that these are acid dissociation constants.) It must be the case that K1 > K2, and that if there is a K3, that K2 > K3. In other words, the first acid dissociation is that of the strongest acidic species of the series; K2 goes with the next strongest acidic species, and so on. In the above phosphate series, the value of pK1 goes with the strongest acid, H3PO4, pK2 goes with H2PO4 – acting as an acid, and pK3 goes with HPO42– acting as an acid. The final species, PO43–, does not have any protons left to give up, so it cannot act as an acid and there is no pK4.
What about the conjugate bases of each of the acidic species? Because of the reciprocal strength relationship between acids and their conjugate bases, the conjugate base of the weakest acid is the strongest base. The weakest acid is HPO42– and its conjugate base is PO43–. Therefore, pKb for PO43–, which is equal to pKw − pKa3 receives the designation pKb1 as −log of the largest basicity constant of the phosphate series:
PO43– + H2O → HPO42– + OH– Kb1 = 10–(pKw – pKa3) = 2.24 × 10−2
Note that we have applied the logarithmic form of one of the relationships given above between Ka and Kb values
Related topics pages: