BIOCHEMISTRY TOPICS
Acid-base chemistry: Part II
Types of pH calculations. Weak acid and weak base equilibria.
Overview of problems in acid-base chemistry
Two broad types of questions tend to arise, for which we will assemble a toolkit
- Given a formal concentration of an acidic or basic species, what is the pH?
- Also, what are the actual concentrations of all species in the equation(s) representing the relevant chemical equilibria?
- Given a fixed pH, and species that can take up or give rise to H+(aq), in what form or forms (protonation states) does the species exist at this pH?
- Principal species analysis. This is to ask which of the forms above is predominant, or present at the highest concentration, at a fixed pH.
- What are the actual concentrations of all species in the equation(s) representing the relevant chemical equilibria? This is the same question as above, but in this case [H+] is a known, fixed quantity.
Our ability to answer these questions rests fundamentally on determination of concentrations of species that are consistent with the equilibrium relations defining Kw and one or more Ka values. While the tools for performing pH calculations are all based upon this general principle, which tool or method we use depends on the specific context. None of the tools is particularly complex mathematically, but care is required to recognize the context and select the appropriate tool. The types of pH calculations can be categorized according to context as follows:
- Strong acid / strong base
- This is the simplest case, where (as we have seen already) we can use pH = −log nF, where F is formal concentration, and n is a stoichiometric coefficient. For a monoprotic acid such as HCl, n = 1. For a strong base, pH = pKw − log nF = 14 − log nF. For a monobasic metal hydroxide such as NaOH, n = 1.
- Weak acid/ weak base
- In this case, the exact solution the equilibrium problem requires solving for the relevant root of a quadratic equation. In many cases, a simple approximation yields satisfactory results.
- Buffers
- A buffer is a mixture of a weak acid and its conjugate base. In this context, the Henderson-Hasselbalch equation is used.
- Intermediate forms of polyprotic acids.
- As we will see, this is the most complex situation in terms of the number of equilibria involved. Fortunately, they are not all independent from one another, and certain simplifying assumptions lead to the equation pH = ½(pKa1 + pKa2).
Definition of Kb and pKb
Kb is known as the base hydrolysis constant, or simply "base constant". It is defined by the chemical equation for abstraction by a base of a proton from water, called the base hydrolysis equation.
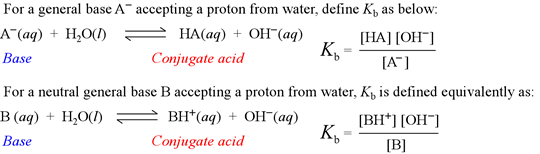
Note that the base hydrolysis equation is a complete Brønsted-Lowry acid-base reaction, with water as the reactant acid. The expression for the base constant is derived by following the usual rules for writing an equilibrium constant for a chemical reaction, with the additional feature that the concentration of water is dropped from the expression. This is because in dilute aqueous solution, the concentration of water remains practically constant.
By analogy to the definition of pH, we define pKb as
pKb = – log Kb
We will use Kb and pKb as a quantitative measures of base strength.
Relationship between Ka, Kb, and Kw
If we combine the general equations defining Ka and Kb, and use the rule for combining equilibrium constants when reactions are summed (the equilibrium constants are multiplied), we obtain a simple and useful relationship between Ka, Kb, and Kw:
HA = H+ + A– Ka = [H+][A– ] / [HA].
A– + H2O = HA + OH – . Kb = [HA][OH –] / [A–].
sum: H2O = H+ + OH – Keq = Ka· Kb = [H+][OH– ] = Kw.
We have derived the relation Kw = Ka· Kb, which hold for aqueous solutions of acids and bases. The logarithmic form of the relation is pKw = pKa + pKb. When the temperature is 25°C, Kw. = 1.0 x 10–14, so that
Ka· Kb = 1.0 x 10–14 (at 25°C), and
pKa + pKb. = 14.00 (at 25°C).
The pH calculation for weak acids and bases
The solution to this problem is generally obtained as the positive root of a quadratic equation. If we let x represent the root to the quadratic equation arising from a weak acid dissociation or weak base hydrolysis reaction with the parameters F (formal concentration of the weak acid or weak base) and K (either Ka for the weak acid, or Kb for the weak base), then we will have an exact solution given as
x = { −K + (K2 + 4KF)1/2 } / 2
For details of how this is obtained, see this example problem. The value of x is then assigned to equilibrium concentrations [H+] and [A−] for the case of the dissociation of a weak acid HA, or to equilibrium concentrations [OH−] and [HA] for the weak base hydrolysis reaction for A−. However, we often make use of an approximation of this solution.
x ≈ (KF)1/2 .
The table below compares the exact versus approximate solutions for several instructive cases.
Weak acid pH calculations: Exact vs approximate solution |
||||||||
formal |
Ka | fraction |
pHexact | pHapprox | ||||
|
0.1 |
10−4 |
0.0311 | 2.507 |
2.500 |
||||
0.1 |
10−5 |
0.00995 (≈ 0.01) | 3.002 |
3.000 |
||||
|
0.1 |
2.63 × 10−4 |
0.05 | 2.301 |
2.290 |
||||
|
0.01 |
10−6 |
0.00995 (≈ 0.01) | 4.002 |
4.000 |
||||
The judgment of whether the approximate value for pH is an adequate substitute for the exact value depends on the context. If one can automatically solve the quadratic equation (using an Excel spreadsheet or programmed calculator), then of course the exact solution would be routinely used since it can be obtained with minimal effort. But if we are forced to calculate pH by hand, it is a considerable savings in labor to use the approximate formula. We can assess the error introduced and decide what fractional or absolute difference between pHapprox and pHexact we are willing to tolerate (for an example of a case where the approximation does not work well, see
Related topics pages: