BIOCHEMISTRY TOPICS
Titrations
Definitions and terminology for titrations. Titration of a strong acid with a strong base. Titration of a weak acid with a strong base. Polyprotic titrations: Titration of the diprotic amino acid glycine.
Acid-base titrations
Titrations, generally speaking, constitute a fundamental technique of analytical chemistry. Here we consider titrations involving an acid and a base. After defining some basic terminology, we proceed with a discussion of three types of acid-base titrations: Titration of a strong acid with a strong base, titration of a weak acid with a strong base, and titration of a weak base with a strong acid. We will want to be able to interpret and construct the graphs of pH versus amount of titrant added, which we refer to as titration curves. Given a facility with the several types of pH calculations (strong-acid/strong-base, weak-acid/weak-base, buffer, intermediate species), and a recognition of which regions in the titration curve a particular type of calculation applies, titration curves for the types of titrations we are considering can be fairly readily predicted.
Definitions
In a titration, the aim is to measure the amount of a known reagent required to react with an unknown amount of a sample" substance. We introduce the following terms and apply them in our discussion and analysis of acid-base titrations.
- Analyte: The substance (in this context, acid or base) to be determined experimentally.
- Titrant: The standardized (i.e. the concentration is known to high accuracy) strong acid or strong base that we add to the analyte in a carefully measured manner.
- Titration curve: The graph obtained when pH is plotted versus the amount of titrant added to the analyte.
- Equivalence point: The point at which the amount of titrant added is exactly equal to the amount of analyte with which it is capable of reacting. The analyte and titrant are at stoichiometric equivalence.
- End point: The observed amount of titrant at which we ascertain the equivalence point has been reached. In acid-base titrations, we look for the end point by means of the color change of an indicator, or the readout of a pH meter.
Titration of a strong acid with a strong base
When a strong acid is titrated with a strong base, a titration curve can be constructed in which the measured pH is plotted against the volume of strong base (titrant) added.
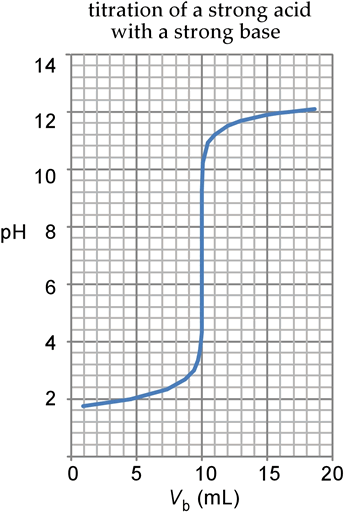
Shown at left is the calculated titration curve for the titration of 50.00 mL of HBr at a concentration of 0.02000 M, using 0.1000 M NaOH as the titrant. We write the reaction in terms of the formulas involved as
HBr(aq) + NaOH(aq) →
NaBr(aq) + H2O(l)
More generally, any strong acid reacting with any strong base will have the common the net ionic equation
H+(aq) + OH –(aq) → H2O(l)
Such a reaction in aqueous solution is practically instantaneous upon mixing.
The equilibrium constant for this reaction is
Keq = 1/Kw = ([ H+ ][ OH – ])–1 = 1.0 × 1014 (at 25°C)
Thus the reaction for all practical purposes goes to completion. The equivalence volume, that is the volume of base added at the equivalence point when mol OH – added = mol H+ present, is 10.00 mL. Since there is no excess of H+ or OH –, the pH must be 7.00, the only source of these ions being autoionization of water.
At other points of the curve, the pH is calculated according to the excess mol of H+ or OH−, the starting pH being 1.669 and the final pH never quite able to reach the pH of the pure base (pH = 13) because of the 50 mL dilution due to the volume of the "analyte". Note the flatness of the curve for volumes other than quite near the equivalence volume, where in contrast the curve is quite steep. There is a dramatic pH change within ± 1 mL of the equivalence volume.
Titration of a weak acid with a strong base
In the case of a titration of a weak acid HA with a strong base such as NaOH, we see a curve similar to that for the titration of a strong acid with a strong base. However, the curve for the titration of a weak acid can be distinguished from that for a strong acid. The principal difference is that the equivalence point is no longer at pH 7, but instead occurs at a pH, on the alkaline side of 7, determined by the strength of the conjugate base A–.
As a specific example, let us consider the titration of the weak acid MES [2-(N-morpholino)ethanesulfonic acid] with the strong base NaOH (sodium hydroxide). The reaction for this titration is shown below. Note that it is the reverse of the base hydrolysis reaction for the conjugate base of MES.
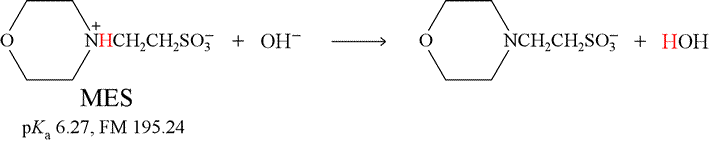
The key point to note is that any hydroxide ion (from NaOH) added to the solution of weak acid reacts completely with MES, converting it to its conjugate base form. As an exercise, you should show that the equilibrium constant for this reaction is quite large, and its value can be calculated as Ka/Kw.
Shown at right is the calculated titration curve for the titration of 50.00 mL of MES at a concentration of 0.02000 M, using 0.1000 M NaOH as the titrant. This example corresponds to that given in §10-2 of Harris (see pp.210-214). Following the discussion there, we distinguish several regions in the graph. These correspond to four different types of calculations used to determine the pH for a given amount of strong base added. (1) When no base has been added (Vb = 0), we have a solution of weak acid. We perform a weak acid calculation, using the formal concentration F and the Ka of the acid. (2) Once some base has been added, some of the HA has been converted into its conjugate base form A–. We can apply the Henderson-Hasselbalch equation in this latter region, which we call the buffer region, using the pKa for the acid and amounts of HA and A−.
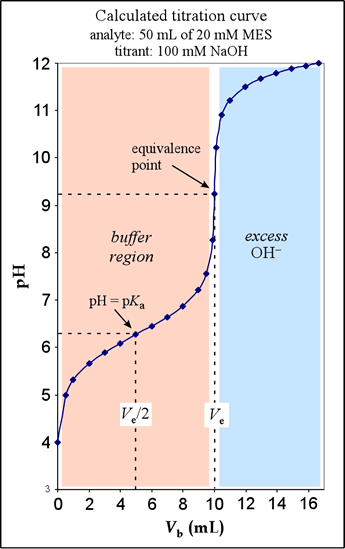
(3) The equivalence point, reached when the amount of strong base added is stoichiometrically equivalent to the amount of HA present to begin with, corresponds to the the complete conversion of HA to A–. Therefore, the pH is calculated as a weak base problem, using a formal concentration F' and Kb of the conjugate base of the weak acid. (4) Past the equivalence point, we are no longer titrating HA, but we are adding excess hydroxide, making pH calculations in this region those we would use for a strong base.
Titration of a weak base with a strong acid
This curve in this case is an inversion and translation of the above - the buffering region would be in the basic pH range, and at the equivalence point, the pH would be less than 7, the titration at that point being a solution of the weak acid conjugate of the base. The calculation types for the four distinct parts of the curve would be as follows: (1) When no acid has been added (Va = 0), we have a solution of weak base. We perform a weak base calculation, using the formal concentration F and the Kb of the base. (2) Once some acid has been added, some of the B has been converted into its conjugate acid form BH+. We can apply the Henderson-Hasselbalch equation in this region, which we call the buffer region, using the pKa for the acid BH+ and amounts of BH+ and B. (3) The equivalence point, reached when the amount of strong acid added is stoichiometrically equivalent to the amount of B present to begin with, corresponds to the the complete conversion of B to BH+. Therefore, the pH is calculated as a weak acid problem, using a formal concentration F' and Ka of the conjugate acid BH+of the weak base B. (4) Past the equivalence point, we are no longer titrating B, but we are adding excess H+, making pH calculations in this region those we would use for a strong acid.
Related topics pages: