BIOCHEMISTRY TOPICS
Intermolecular forces
Types of intermolecular forces and their strengths.
van der Waals interactions
Attractive forces exist between all atoms and molecules, regardless of their charges or electronegativities. Atoms and molecules are all - to varying extents - polarizable, meaning that the electronic charge distribution of the atom or molecule is altered in response to the presence of an electric field. The electric field may arise from a nearby charge, dipole, or a transient dipole due to the fluctuating electron distributions in even a nonpolar molecule. The significance of polarizability from the standpoint of non-covalent interactions is that the resulting induced dipole always interacts favorably with the field that produced it.
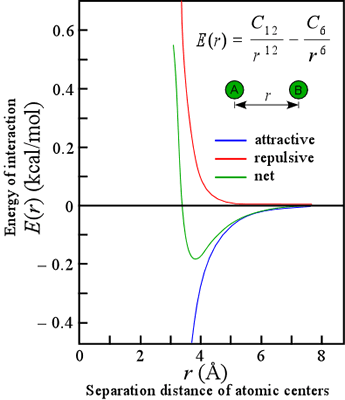
The attractive forces that arise from induced polarization are collectively referred to as van der Waals interactions. They are very short-range, in that the energy of such interaction varies inversely with the sixth power of the distance of separation (see equation). There are actually three types of van der Waals interactions: those between two preexisting dipoles, between an existing dipole and an induced dipole, and between two mutually induced dipoles. These latter interactions are usually what come to mind when we think of van der Waals interactions, which are the only kind of attractive force between nonpolar molecules. These are technically known as London or dispersion forces.
Our discussion of van der Waals interactions is simplified by taking a classical view of the atom, whereas the quantum mechanical nature of dispersion forces makes them inherently complex. The van der Waals interactions are often represented in an equation that includes a repulsive term due to unfavorable contacts between the electron "clouds" of atoms at close range. The most common form of this energy potential is the Lennard-Jones 6,12 potential, represented in the equation. Note that the energetically optimal distance is typically 0.3 - 0.5 Å greater than the sum of the so-called van der Waals radii measured from closest contact distances in crystals. (For more information, see Creighton, i. e. the reference listed below, pp.145-146, from which this discussion has been adapted.)
Reference
Creighton, TE. Proteins: Structure and Molecular Properties (2nd ed, 1993. Freeman)
Electrostatic interactions
Charges on functional groups result from ionizations or proton transfers. In addition, the unequal distribution of electrons in covalent bonds between atoms of different electronegativity creates electric dipoles in molecules. The arrangement of charges and dipoles in a molecule creates a particular distribution of electric potential energy, and this distribution can in theory be expressed mathematically by an electric potential energy function.
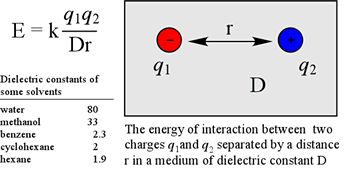
The simplest case is the energy due to two point charges, q1 and q2, separated by a distance r, in a medium with dielectric constant D. In this case, the energy is given by the equation at left. The value of the constant k of proportionality depends on the units involved. One problem with applying the equation above to protein structures is that the dielectric constant D is only well-defined as bulk property, e.g. in a homogeneous liquid.
With reference to protein structure, the effective dielectric constant can vary dramatically within the space of a few tens of angstroms, as when one traverses the interface between an aqueous environment, and the non-polar interior of a folded protein. While a dielectric constant near 80 governs the strength of electrostatic interactions in aqueous solution and between groups in solvent-accessible regions of proteins, a value of D corresponding to a nonpolar liquid such as hexane is often used to model the strength of electrostatic force in nonpolar regions within the core of a folded protein. One consequence of a relatively large dielectric constant, like that of water is that the strength of electrostatic forces are dampened. Conversely, the force between charges within a low dielectric medium is correspondingly larger.
Also included in the category of electrostatic forces are those associated between point charges and dipoles, dipole-dipole interactions (illustrated in the figure below), and more complex patterns of charge distribution such as quadrupoles. The equations governing the energies associated with such interactions are more complex than the one given above for point charges. These interactions are in general somewhat weaker than those between point charges, fall off more quickly with distance, and also show dependence on relative orientation of the charge separations.
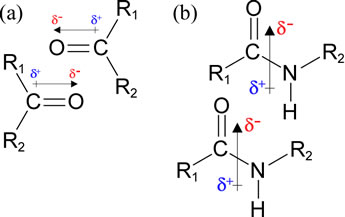
The figure at left shows favorable (low energy) alignments of permanent dipoles associated with (a) carbonyl groups, and (b) peptide groups. The arrows with the hatched tails show the way the dipoles are represented as dipole moment vectors. The direction and magnitude is determined by the amount and orientation of charge separation (polarization). For the bonding between two atoms, this polarization can be evaluated as the difference in electronegativity between the pair of bonded atoms. For a polyatomic grouping (as in b), the dipole moment arises as the vector sum of individual bond dipoles. The δ notation indicates the magnitude of charge polarization, a quantity that is typically some fraction of the charge of an electron or proton. These are examples of dipole-dipole interactions that occur in biomolecules. They are fundamentally a type electrostatic interaction, however these are distinct (and weaker than) charge-charge interactions, or ion pairs. The charges in this case are monopolar, and are a full (or some multiple of) atomic (electron/proton) charge unit. Like a charge-charge interaction, we would expect that the energy of interaction to become much less favorable with a small increase in r, the distance of separation. However, unlike the interaction between point charges, favorable dipole-dipole interaction energies become less so more steeply with increasing r distance and are - like a compass needle - highly orientation dependent (a modest change in the angle of orientation between the dipole vectors changes the energy dramatically).
Hydrogen bonds
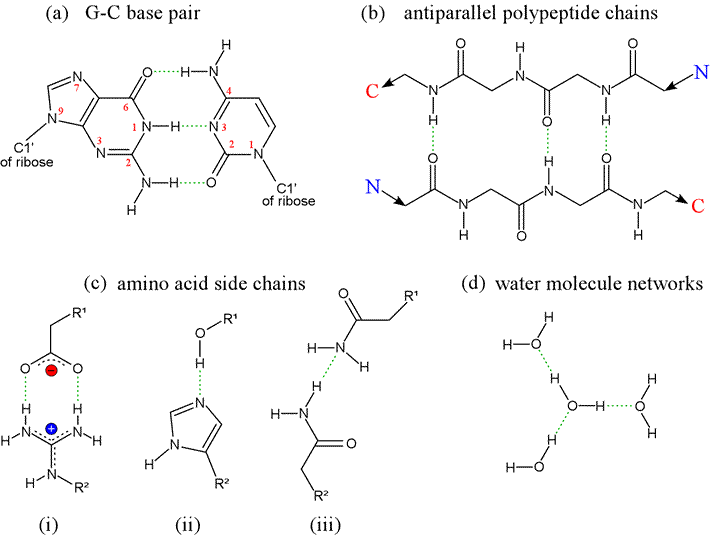
Hydrogen bonds arise from the interaction between a hydrogen atom covalently bonded to an electronegative atom - typically oxygen or nitrogen - and an unshared pair of electrons from another electronegative atom (also typically O or N). In the classic form of the hydrogen bond, although the H atom is in a sense shared between the two electronegative atoms, it is not shared equally, being covalently bound to one (designated the donor) while interacting strongly with the other atom (called the acceptor) because of the strong dipoles involved. The forces arising from point charges, dipoles, hydrogen bonds, and van der Waals interactions are alike in that they share a fundamentally electrostatic nature. In contrast to forces between point charges however, which depend on distance of separation, hydrogen bonds are highly directional.
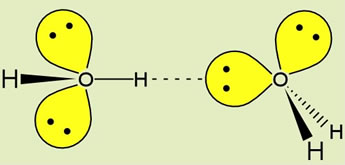
Note that water is the hydrogen bonding solvent par excellence, since each water possesses two donor groups (-OH) and two acceptor groups (:O). At left, the geometry of a hydrogen bond between two water molecules, illustrating the orientation of the covalent bonds and oxygen sp3 orbitals containing nonbonding electron pairs. The ideal hydrogen bond forms when the O-H donor group and the lone pair sp3 orbital of the acceptor are aligned along a straight line.
Related topics pages: